题目内容
1.已知函数f(x)=px-$\frac{4p}{x}$-lnx,g(x)=lnx-$\frac{p}{x}$(4+$\frac{{e}^{2}-2e}{{p}^{2}}$),其中无理数e=2.71828…(1)若p=0,求证:f(x)≥1-x;
(2)若f(x)在其定义域是单调函数,求实数p的取值范围;
(3)对于区间(1,2)中的任意常数p,是否存在x0>0使f(x0)≤g(x0)成立?若存在,求出符合条件的x0;否则,说明理由.
分析 (1)若P=0,要证f(x)≥1-x;即可转化为lnx-x+1≥0在定义域内恒成立即可.在通过求导,研究其单调性,看函数的最小值,只要函数的最小值大于等于0即可.
(2)若在其定义域内f(x)是单调函数,求P的取值范围;先要明确定义域;在求导,求导后,只要满足导数在某区间恒大于0或在某区间恒小于0即可.在这里要注意对参数p进行讨论.
(3)对于区间(1,2)中的任意常数P,是否存在x0>0,使f(x0)≤g(x0)成立,这种题型属探索性问题;解决的关键在于弄懂题意.据题意可转化为:令F(x)=f(x)-g(x)=px-2lnx+$\frac{{e}^{2}-2e}{px}$,则问题等价于找一个x0>0使F(x)≤0成立,故只需满足函数的最小值F(x)min≤0即可.
解答 解:(Ⅰ)证明:当p=0时,f(x)=-lnx.
令m(x)=lnx-x+1,则m′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$.
若0<x<1,m′(x)>0,m(x)递增;
若x>1,m′(x)<0,m(x)递减,
则x=1是m(x)的极(最)大值点.
于是m(x)≤m(1)=0,即lnx-x+1≤0.
故当p=0时,有f(x)≥1-x;
(2)对f(x)=px-$\frac{4p}{x}$-lnx求导,
得f′(x)=p+$\frac{4p}{{x}^{2}}$-$\frac{1}{x}$=$\frac{{px}^{2}-x+4p}{{x}^{2}}$.
①若p=0,f′(x)=-$\frac{1}{x}$<0,
则f(x)在(0,+∞)上单调递减,故p=0合题意.
②若p>0,h(x)=px2-x+4p=p(x-$\frac{1}{2p}$)2+4p-$\frac{1}{4p}$≥4p-$\frac{1}{4p}$.
则必须4p-$\frac{1}{4p}$≥0,f′(x)≥0,
故当p≥$\frac{1}{4}$时,f(x)在(0,+∞)上单调递增.
③若p<0,h(x)的对称轴x=$\frac{1}{2p}$<0,
则必须h(0)≤0,f′(x)≤0,
故当p<0时,f(x)在(0,+∞)上单调递减.
综合上述,p的取值范围是(-∞,0]∪[$\frac{1}{4}$,+∞);
(3)令F(x)=f(x)-g(x)=px-2lnx+$\frac{{e}^{2}-2e}{px}$.
则问题等价于找一个x0>0使F(x)≤0成立,
故只需满足函数的最小值F(x)min≤0即可.
因F′(x)=p-$\frac{2}{x}$-$\frac{{e}^{2}-2e}{{px}^{2}}$=$\frac{(px-e)(px-2+e)}{{px}^{2}}$=$\frac{p}{{x}^{2}}$(x-$\frac{e}{p}$)(x-$\frac{2-e}{p}$),
而x>0,1<p<2,$\frac{e}{p}$>$\frac{2}{p}$>0,$\frac{2-e}{p}$<0,
故当0<x<$\frac{e}{p}$时,F′(x)<0,F(x)递减;
当x>$\frac{e}{p}$时,F′(x)>0,F(x)递增.
于是,F(x)min=F($\frac{e}{p}$)=e-2+2lnp+e-2=2e+2lnp-4>0.
与上述要求F(x)min≤0相矛盾,故不存在符合条件的x0.
点评 (1)若在其定义域内f(x)是单调函数,求参数的取值范围;先要明确定义域;在求导,求导后,只要满足导数在某区间恒大于0或在某区间恒小于0即可.这是通性通法.
(2)对于区间任意给定的某区间,某代数式恒成立问题,解决的关键在于弄懂题意.据题意一般可可转化为构造一个函数,求满足函数的最小值或者函数的最大值即可

| A. | $\sqrt{5}$ | B. | $\sqrt{29}$ | C. | $3\sqrt{2}$ | D. | 4 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 第4名学生操作了n台设备 | B. | 第4名学生操作了3台设备 | ||
| C. | 第3名学生操作了n台设备 | D. | 第3名学生操作了4台设备 |
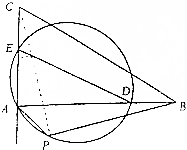 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.