题目内容
18.已知函数y=a${\;}^{{x}^{2}-4x+1}$(0<a<1),求函数的单调区间及值域.分析 设t=x2-4x+1,利用换元法结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=x2-4x+1,则t=(x-2)2-3,
对称轴为x=2,
∵0<a<1,
∴y=at为减函数,
当x≥2时,函数t=x2-4x+1为增函数,
∵y=at为减函数,∴y=a${\;}^{{x}^{2}-4x+1}$为减函数,即单调递减区间为[2,+∞),
当x≤2时,函数t=x2-4x+1为减函数,
∵y=at为减函数,∴y=a${\;}^{{x}^{2}-4x+1}$为增函数,即单调递增区间为(-∞,2].
∵t=(x-2)2-3≥-3,
∴y=at≤a-3,
∵y=at>0,
∴0<y≤a-3,
即函数的值域为(0,a-3].
点评 本题主要考查函数单调性的求解,利用换元法结合复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知f(x)=-x+sinx,命题p:?x∈(0,$\frac{π}{2}$),f(x)<0,则( )
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |
6.某学校高二学生进行研究性学习,某班共有m(m∈N*)名学生编号为1、2、3…m,有n(n∈N*)台设备编号分别为1、2、3…n,定义记号aij;如果第i名学生操作了第j台设备,此时规定aij=1否则aij=0,则等式a41+a42+a43+…a4n=3的实际意义为( )
| A. | 第4名学生操作了n台设备 | B. | 第4名学生操作了3台设备 | ||
| C. | 第3名学生操作了n台设备 | D. | 第3名学生操作了4台设备 |
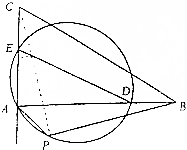 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.