题目内容
已知椭圆Γ的方程为 ,A(0,b)、B(0,-b)和Q(a,0)为Γ的三个顶点.
,A(0,b)、B(0,-b)和Q(a,0)为Γ的三个顶点.(1)若点M满足
 ,求点M的坐标;
,求点M的坐标;(2)设直线l1:y=k1x+p交椭圆Γ于C、D两点,交直线l2:y=k2x于点E.若
 ,证明:E为CD的中点;
,证明:E为CD的中点;(3)设点P在椭圆Γ内且不在x轴上,如何构作过PQ中点F的直线l,使得l与椭圆Γ的两个交点P1、P2满足

 ?令a=10,b=5,点P的坐标是(-8,-1),若椭圆Γ上的点P1、P2满足
?令a=10,b=5,点P的坐标是(-8,-1),若椭圆Γ上的点P1、P2满足 ,求点P1、P2的坐标.
,求点P1、P2的坐标.
【答案】分析:(1)由题意知M是B(0,-b)和Q(a,0)的中点,所以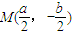 .
.
(2)由题设条件得方程(a2k12+b2)x2+2a2k1px+a2(p2-b2)=0,所以a2k12+b2-p2>0是CD的中点;
(3)因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由 知F为P1P2的中点,由此可得P1(-6,-4)、P2(8,3).
知F为P1P2的中点,由此可得P1(-6,-4)、P2(8,3).
解答:解:(1)∵ ,
,
∴M是B(0,-b)和Q(a,0)的中点,
∴ .
.
(2)由方程组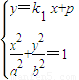 ,
,
消y得方程(a2k12+b2)x2+2a2k1px+a2(p2-b2)=0,
因为直线l1:y=k1x+p交椭圆Γ于C、D两点,
所以△>0,即a2k12+b2-p2>0,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),
则 ,
,
由方程组 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,
又因为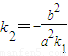 ,
,
所以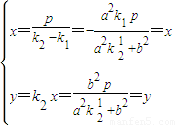 ,
,
故E为CD的中点;
(3)因为点P在椭圆Γ内且不在x轴上,
所以点F在椭圆Γ内,可以求得直线OF的斜率k2,
由 知F为P1P2的中点,
知F为P1P2的中点,
根据(2)可得直线l的斜率 ,
,
从而得直线l的方程.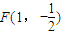 ,
,
直线OF的斜率 ,
,
直线l的斜率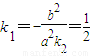 ,
,
解方程组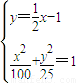 ,消y:x2-2x-48=0,
,消y:x2-2x-48=0,
解得P1(-6,-4)、P2(8,3),或P1(8,3)、P2(-6,-4),.
点评:本题考查直线的圆锥曲线的综合问题,解题时要注意公式的灵活运用.
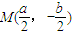 .
.(2)由题设条件得方程(a2k12+b2)x2+2a2k1px+a2(p2-b2)=0,所以a2k12+b2-p2>0是CD的中点;
(3)因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由
 知F为P1P2的中点,由此可得P1(-6,-4)、P2(8,3).
知F为P1P2的中点,由此可得P1(-6,-4)、P2(8,3).解答:解:(1)∵
 ,
,∴M是B(0,-b)和Q(a,0)的中点,
∴
 .
.(2)由方程组
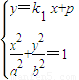 ,
,消y得方程(a2k12+b2)x2+2a2k1px+a2(p2-b2)=0,
因为直线l1:y=k1x+p交椭圆Γ于C、D两点,
所以△>0,即a2k12+b2-p2>0,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),
则
 ,
,由方程组
 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,又因为
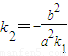 ,
,所以
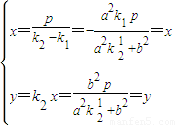 ,
,故E为CD的中点;
(3)因为点P在椭圆Γ内且不在x轴上,
所以点F在椭圆Γ内,可以求得直线OF的斜率k2,
由
 知F为P1P2的中点,
知F为P1P2的中点,根据(2)可得直线l的斜率
 ,
,从而得直线l的方程.
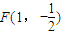 ,
,直线OF的斜率
 ,
,直线l的斜率
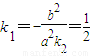 ,
,解方程组
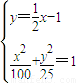 ,消y:x2-2x-48=0,
,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3),或P1(8,3)、P2(-6,-4),.
点评:本题考查直线的圆锥曲线的综合问题,解题时要注意公式的灵活运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
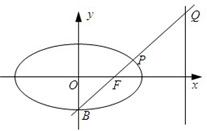 如图,已知椭圆C的方程为:
如图,已知椭圆C的方程为: 已知椭圆C的方程为
已知椭圆C的方程为