题目内容
 如图,已知椭圆C的方程为:
如图,已知椭圆C的方程为:| x2 |
| a2 |
| y2 |
| b2 |
分析:根据B,F点坐标可知直线BP的方程,进而根据P恰好是BQ的中点求得P点横坐标,代入直线方程后求得P点纵坐标代入椭圆方程即可求得a和c的关系,进而求得椭圆的离心率.
解答:解:依题意可知直线BP的方程为y=
x-b,
∵P恰好是BQ的中点,∴xp=
,
∴yp=b(
-1)代入椭圆方程得
+(
-1)2=1,
解得
=
,
∴椭圆的离心率为
=
,
故答案为
.
| b |
| c |
∵P恰好是BQ的中点,∴xp=
| a2 |
| 2c |
∴yp=b(
| a2 |
| 2c 2 |
| a2 |
| 4c2 |
| a2 |
| 2c2 |
解得
| a |
| c |
| 3 |
∴椭圆的离心率为
| c |
| a |
| ||
| 3 |
故答案为
| ||
| 3 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知椭圆C的方程为
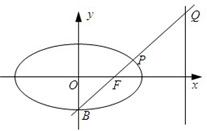
如图,已知椭圆C的方程为 (a>b>0),B是它的下顶点,F是其右焦点,BF的延长线与椭圆及其右准线分别交于P、Q两点,若点P恰好是BQ的中点,则此椭圆的离心率是 .
(a>b>0),B是它的下顶点,F是其右焦点,BF的延长线与椭圆及其右准线分别交于P、Q两点,若点P恰好是BQ的中点,则此椭圆的离心率是 .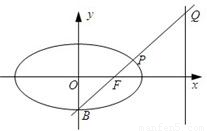
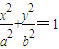 (a>b>0),B是它的下顶点,F是其右焦点,BF的延长线与椭圆及其右准线分别交于P、Q两点,若点P恰好是BQ的中点,则此椭圆的离心率是 .
(a>b>0),B是它的下顶点,F是其右焦点,BF的延长线与椭圆及其右准线分别交于P、Q两点,若点P恰好是BQ的中点,则此椭圆的离心率是 .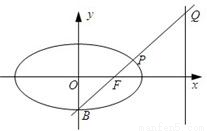
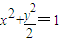 ,点P(a,b)的坐标满足
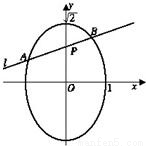
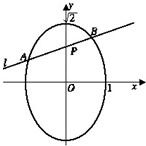
,点P(a,b)的坐标满足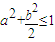 ,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求: