题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+3,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,直线y=k与函数f(x)的图象相交于四个不同的点,交点的横坐标依次记为a,b,c,d,则abcd的取值范围是[0,e4).分析 画出y=f(x)与y=k的图象,运用韦达定理和对数的运算性质,计算即可得到所求范围.
解答 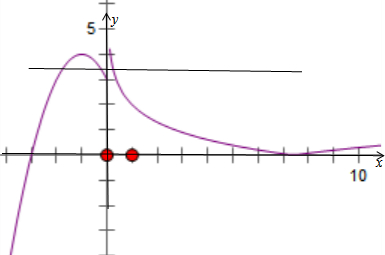 解:函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+3,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,的图象如下:
解:函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+3,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,的图象如下:
四个交点横坐标从小到大,依次记为a,b,c,d,
则a,b是x2+2x+k-3=0的两根,
由于x<0时,
-x2-2x+3=4-(x+1)2≤4,
判别式为4-4(k-3)=4(4-k)>0,
即有k<4,
∴a+b=-2,ab=k-3<1,
∴ab∈[0,1),
且lnc=2-k,lnd=2+k,
∴ln(cd)=4,∴cd=e4,
∴abcd∈[0,e4),
故答案为:[0,e4).
点评 本题考查函数的图象,分段函数,零点与方程的根之间的关系,综合性较强.

练习册系列答案
相关题目
5.已知等差数列{an},Sn是其前n项的和,若S3=2a3,则$\frac{{{S_{2015}}}}{{{a_{2015}}}}$的值为( )
| A. | 2015 | B. | 2016 | C. | 1024 | D. | 1008 |
15.在等比数列{an}中,a1+a2=72,a3+a4=18,那么a4+a5=( )
| A. | 6 | B. | 9 | C. | ±6 | D. | ±9 |
20.在△ABC中,若b=2asinB,则A为 ( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2}{3}π$ | D. | $\frac{5}{6}π$或$\frac{π}{6}$ |