题目内容
【题目】等比数列{an}中，a1=2，a4=16．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若a3 ， a5分别为等差数列{bn}的第4项和第16项，试求数列{bn}的前项和Sn ．
【答案】解：（Ⅰ）设{an}的公比为q，
由已知得16=2q3 ， 解得q=2．
又a1=2，所以 
．
（Ⅱ）由（I）得a3=8，a5=32，则b4=8，b16=32．
设{bn}的公差为d，则有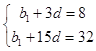 
，解得 
．
则数列{bn}的前项和 
【解析】（Ⅰ）由首项和第四项代入等比数列通项公式求出公比，然后直接写出通项公式；（Ⅱ）求出a2和a5 ， 即得到等差数列{bn}的第4项和第16项，设出公差后列方程组可求等差数列{bn}的首项和公差，则前n项和可求．
【考点精析】根据题目的已知条件，利用等差数列的前n项和公式和等比数列的通项公式（及其变式）的相关知识可以得到问题的答案，需要掌握前n项和公式：
；通项公式：
．
练习册系列答案
相关题目
