题目内容
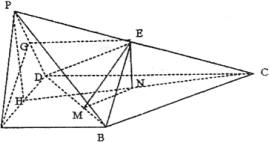
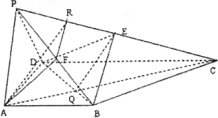
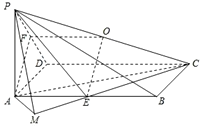
已知在四棱锥P－ABCD中，底面ABCD是直角梯形，∠BAD＝90°，2AB＝2AD＝CD，侧面PAD是正三角形且垂直于底面ABCD，E是PC上一点．
(1)点E是PC中点时，求证：BE⊥平面PCD；
(2)在(1)的条件下，求二面角C－BD－E的大小；
(3)当E是PC中点时，在PB上是否存在一点F，使AF∥平面BDE.若存在，请确定点F的位置；若不存在，请说明理由．
答案：
解析：
解析：
|
(1)证明：取PD中点G，连EG、AG，则∵△PAD是正三角形，∴AG⊥PD，又易知 CD⊥平面PAD，∴AG⊥CD， ∴AG⊥平面PCD. 又∵EG∥CD∥AB，且EG= ∴BE∥AG，从而BE⊥平面PCD. (2)
解：取AD中点H，连结PH、HC， 取HC中点N，过N作MN⊥BD于点M，连ME. 由条件易得：PH⊥平面ABCD，又N、E分别是HC和PC的中点，∴EN⊥平面ABCD，则由三垂线定理得：EM⊥BD，故∠EMN就是所求二面角的平面角.设AB=AD=a，则 ∴在Rt△EMN中， (3)存在PB中点F，使AF∥平面BDE. 证明：连结AC交BD于点Q，取PE中点R，连结FR， ∵AQ：QC=AB：CD=1：2，RE：EC=1：2， ∴AR∥QE，∴AR∥平面BDE，又RF∥BE， ∴RF∥平面BDE．∴平面AEF∥平面BDE |
，
，
，
，∴所求二面角的大小为
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
已知在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD的中点．
（2012•即墨市模拟）已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2a，AB=a，PA⊥平米ABCD，F是线段BC的中点．H为PD中点．
（2012•即墨市模拟）已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2a，AB=a，PA⊥平米ABCD，F是线段BC的中点．H为PD中点．
如图，已知在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥底面ABCD，AB=1，PA•AC=1，∠ABC=θ（0＜θ＜
（2012•枣庄二模）已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．