题目内容
已知向量 =(k,12),
=(k,12), =(4,5),
=(4,5), =(10,k).
=(10,k).
(1)若A,B,C三点共线,求实数k的值;
(2)若A,B,C构成直角三角形,求实数k的值.
解:(1)若A,B,C三点共线,则 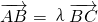 ,λ 为非零实数.
,λ 为非零实数.
即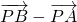 =λ (
=λ (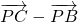 ),∴(4-k,-7)=λ(6,k-5),∴4-k=6λ,-7=λ(k-5),
),∴(4-k,-7)=λ(6,k-5),∴4-k=6λ,-7=λ(k-5),
解得 k=11,或 k=-2.
(2)若A,B,C构成直角三角形,由(1)可得 =(4-k,-7),
=(4-k,-7), =(6,k-5),
=(6,k-5),
 =
= -
- =(10-k,k-12).
=(10-k,k-12).
当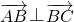 时,由
时,由 =6(4-k)-7(k-5)=0,可得 k=
=6(4-k)-7(k-5)=0,可得 k=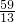 .
.
当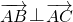 时,由
时,由 =(4-k,-7)(10-k,k-12)=0,可得 k 无解.
=(4-k,-7)(10-k,k-12)=0,可得 k 无解.
当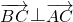 时,由
时,由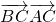 =(6,k-5)(10-k,k-12)=0,解得 k=8,或k=15.
=(6,k-5)(10-k,k-12)=0,解得 k=8,或k=15.
综上,实数k的值为: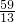 ,8,15.
,8,15.
分析:(1)若A,B,C三点共线,则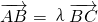 ,λ 为非零实数,由 (4-k,-7)=λ(6,k-5),求出k 的值.
,λ 为非零实数,由 (4-k,-7)=λ(6,k-5),求出k 的值.
(2)分别由 =0、
=0、 =0、
=0、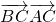 =0,解方程求出实数k的值.
=0,解方程求出实数k的值.
点评:本题考查两个向量共线的性质,两个向量坐标形式的运算,两个向量垂直的性质,是一道中档题.
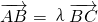 ,λ 为非零实数.
,λ 为非零实数.即
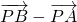 =λ (
=λ (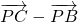 ),∴(4-k,-7)=λ(6,k-5),∴4-k=6λ,-7=λ(k-5),
),∴(4-k,-7)=λ(6,k-5),∴4-k=6λ,-7=λ(k-5),解得 k=11,或 k=-2.
(2)若A,B,C构成直角三角形,由(1)可得
 =(4-k,-7),
=(4-k,-7), =(6,k-5),
=(6,k-5), =
= -
- =(10-k,k-12).
=(10-k,k-12).当
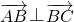 时,由
时,由 =6(4-k)-7(k-5)=0,可得 k=
=6(4-k)-7(k-5)=0,可得 k=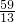 .
.当
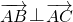 时,由
时,由 =(4-k,-7)(10-k,k-12)=0,可得 k 无解.
=(4-k,-7)(10-k,k-12)=0,可得 k 无解.当
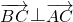 时,由
时,由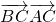 =(6,k-5)(10-k,k-12)=0,解得 k=8,或k=15.
=(6,k-5)(10-k,k-12)=0,解得 k=8,或k=15.综上,实数k的值为:
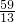 ,8,15.
,8,15.分析:(1)若A,B,C三点共线,则
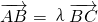 ,λ 为非零实数,由 (4-k,-7)=λ(6,k-5),求出k 的值.
,λ 为非零实数,由 (4-k,-7)=λ(6,k-5),求出k 的值.(2)分别由
 =0、
=0、 =0、
=0、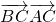 =0,解方程求出实数k的值.
=0,解方程求出实数k的值.点评:本题考查两个向量共线的性质,两个向量坐标形式的运算,两个向量垂直的性质,是一道中档题.

练习册系列答案
相关题目
已知向量
=(k,12),
=( 4,5 ),
=(-k,10 ),且A、B、C三点共线,则 k 的值是( )
| OA |
| OB |
| OC |
A、-
| ||
B、
| ||
C、
| ||
D、
|