题目内容

已知向量
PA
=（k，12），
PB
=（4，5），
PC
=（10，k）．
（1）若A，B，C三点共线，求实数k的值；
（2）若A，B，C构成直角三角形，求实数k的值．
分析：（1）若A，B，C三点共线，则
AB
= λ •
BC
，λ 为非零实数，由 （4-k，-7）=λ（6，k-5），求出k 的值．
（2）分别由
AB
•
BC
=0、
AB
•
AC
=0、
BC
•
AC
=0，解方程求出实数k的值．
解答：解：（1）若A，B，C三点共线，则
AB
= λ •
BC
，λ 为非零实数．
即
PB
 -
PA
=λ （
PC
-
PB
 ），∴（4-k，-7）=λ（6，k-5），∴4-k=6λ，-7=λ（k-5），
解得 k=11，或 k=-2．
（2）若A，B，C构成直角三角形，由（1）可得
AB
=（4-k，-7），
BC
=（6，k-5），
AC
=
PC
-
PA
=（10-k，k-12）．
当
AB
⊥
BC
 时，由
AB
•
BC
=6（4-k）-7（k-5）=0，可得 k=
59
13
．
当
AB
⊥
AC
时，由
AB
•
AC
=（4-k，-7）（10-k，k-12）=0，可得 k 无解．
当
BC
⊥
AC
时，由
BC
•
AC
=（6，k-5）（10-k，k-12）=0，解得 k=8，或k=15．
综上，实数k的值为：
59
13
，8，15．
点评：本题考查两个向量共线的性质，两个向量坐标形式的运算，两个向量垂直的性质，是一道中档题．
练习册系列答案
相关题目

如图，已知PA⊥平面ABCD，四边形ABCD为正方形，G为△PDC的重心，＝i，＝j，＝k，试用基底{i，j，k}表示向量，．

本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分.作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。K^S*5U.C#O
（1）（本小题满分7分）选修4-2：矩阵与变换
已知向量=，变换T的矩阵为A=，平面上的点P（1，1）在变换T
作用下得到点P′（3，3），求A4.
（2）（本小题满分7分）选修4-4：坐标系与参数方程
直线与圆（>0）相交于A、B两点，设
P（－1，0），且|PA|:|PB|=1:2，求实数的值
（3）（本小题满分7分）选修4-5：不等式选讲K^S*5U.C#O
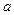对于x∈R，不等式|x－1|+|x－2|≥2+2恒成立，试求2+的最大值。
如图,已知PA⊥平面ABCD,四边形ABCD为正方形,G为△PDC的重心,=i,=j,=k,试用基底｛i,j,k｝表示向量,.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网