题目内容
9.已知正方形ABCD,M是DC的中点,由$\overrightarrow{AM}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$确定m,n的值,计算定积分 ${∫}_{mπ}^{nπ}$sinxdx=1.分析 先根据向量的意义求出m,n的值,再根据定积分的计算法计算即可.
解答 解:∵$\overrightarrow{AM}$=$\overrightarrow{AD}$+$\overrightarrow{DM}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{DC}$=$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{AB}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AB}$=-$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{AC}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,
∴m=-$\frac{1}{2}$,n=1,
∴${∫}_{mπ}^{nπ}$sinxdx=${∫}_{-\frac{π}{2}}^{π}$sinxdx=-cosx|${\;}_{-\frac{π}{2}}^{π}$=1,
故答案为:1.
点评 本题考查了向量的几意义以及定积分的计算,属于基础题.

练习册系列答案
相关题目
4.在不等式组$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥0}\\{y≤a}\end{array}\right.$确定的平面区域中,若z=x+2y的最大值为9,则a的值为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
14.已知α为第二象限角,cos2α=-$\frac{\sqrt{5}}{3}$,则sinα-cosα=( )
| A. | $\frac{\sqrt{15}}{3}$ | B. | $\frac{\sqrt{15}}{3}$或$\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{3}}{9}$ |
18.在求2+5+8+…+2015的程序框图中(如图),正整数m的最大值为( )


| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
 在数学活动中,小明为了求$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形.请你利用这个几何图形,求$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为$1-\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形.请你利用这个几何图形,求$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为$1-\frac{1}{{2}^{n}}$.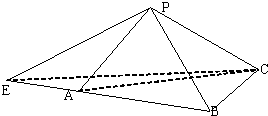 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.
如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.