题目内容
【题目】己知抛物线C：x2=4y的焦点为F，直线l与抛物线C交于A，B两点，延长AF交抛物线C于点D，若AB的中点纵坐标为|AB|-1，则当∠AFB最大时，|AD|=（ ）
A. 4B. 8C. 16D. 
【答案】C
【解析】
设出A，B，D的坐标，利用抛物线定义可得|AF|+|BF|=2|AB|，再由余弦定理写出cos∠AFB，利用基本不等式求最值，可得当∠AFB最大时，△AEB为等边三角形，得到AF所在直线方程，再与抛物线方程联立，结合根与系数的关系及抛物线定义求得|AD|．
解：
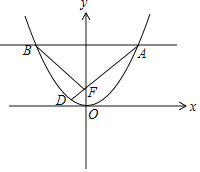
设A（x1，y1），B（x2，y2），D（x3，y3），
由抛物线定义得：y1+y2+2=|AF|+|BF|，
，
，当且仅当|AF|=|BF|时取等号．
∴当∠AFB最大时，△AFB为等边三角形，
联立
，
，消去y，得
．
．
∴|AD|=16．
故选：C．
练习册系列答案
相关题目
