题目内容
已知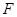 为双曲线
为双曲线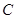 :
: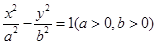 的右焦点,
的右焦点,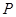 为双曲线
为双曲线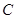 右支上一点,
右支上一点,
且位于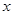 轴上方,
轴上方,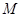 为直线
为直线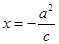 上一点,
上一点,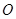 为坐标原点,已知
为坐标原点,已知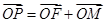 ,
,
且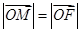 ,则双曲线
,则双曲线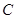 的离心率为
的离心率为
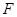 为双曲线
为双曲线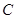 :
: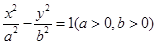 的右焦点,
的右焦点,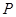 为双曲线
为双曲线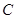 右支上一点,
右支上一点,且位于
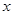 轴上方,
轴上方,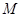 为直线
为直线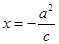 上一点,
上一点,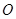 为坐标原点,已知
为坐标原点,已知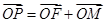 ,
,且
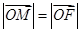 ,则双曲线
,则双曲线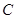 的离心率为
的离心率为 A. | B. | C. | D. |
A
分析:先确定M的坐标,再确定P的坐标,代入双曲线方程,即可求得结论.
解:由题意,M位于x轴上方
∵|
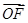 |=|
|=|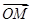 |,M为直线x=-
|,M为直线x=-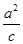 上一点
上一点∴M(-
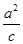 ,
,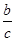
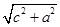 )
)∵
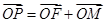
∴四边形OMPF为菱形
∴P(c-
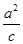 ,
,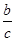
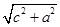 ),即P(
),即P(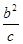 ,
,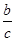
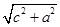 )
)代入双曲线方程可得
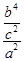 -
-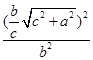 =1
=1化简可得c2=4a2
∴c=2a,
∴e=
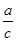 =2
=2故选A.

练习册系列答案
相关题目
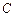 :
: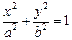 (
(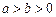 ),其焦距为
),其焦距为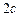 ,若
,若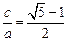 (
(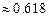 ),则称椭圆
),则称椭圆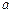 、
、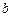 、
、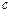 成等比数列.
成等比数列.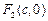 ,
,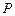 为椭圆
为椭圆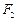 、
、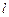 ,使
,使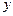 轴的交点
轴的交点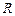 满足
满足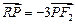 ?若存在,求直线
?若存在,求直线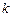 ;若不存在,请说明理由.
;若不存在,请说明理由.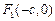 、
、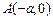 、
、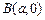 、
、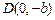 、
、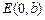 为顶点的菱形
为顶点的菱形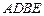 的内切圆过焦点
的内切圆过焦点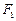 、
、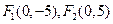 ,点
,点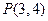
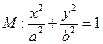
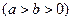 的离心率为
的离心率为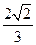 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为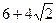 .
.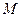 的方程;
的方程;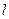 与椭圆
与椭圆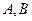 两点,且以
两点,且以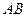 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点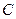 ,
,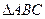 面积的最大值.
面积的最大值.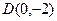 ,过点
,过点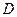 作抛物线
作抛物线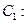
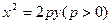 的切线
的切线 ,切点
,切点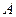 在第二象限,如图.(Ⅰ)求切点
在第二象限,如图.(Ⅰ)求切点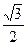 的椭圆
的椭圆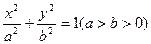 恰好经过切点
恰好经过切点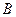 ,记切线
,记切线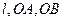 的斜率分别为
的斜率分别为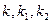 ,若
,若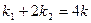 ,求椭圆方程.
,求椭圆方程.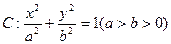 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=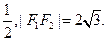
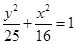 的离心率等于( ).
的离心率等于( ).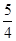



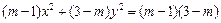 表示椭圆,则
表示椭圆,则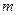 的取值范围为 .
的取值范围为 .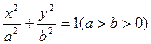 经过点
经过点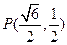 ,离心率为
,离心率为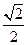 ,动点
,动点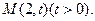
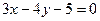 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;