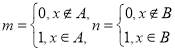题目内容
【题目】过抛物线![]() 的焦点
的焦点![]() 作倾斜角为45°的直线
作倾斜角为45°的直线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,若
,若![]() .
.
(1)抛物线![]() 的方程;
的方程;
(2)若经过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据题意可得直线![]() 的方程为
的方程为![]() ,再根据韦达定理结合
,再根据韦达定理结合![]() ,即可求出;
,即可求出;
(2)当直线的斜率不存在求出![]() ,当直线的斜率存在,根据韦达定理和中点坐标公式,根据
,当直线的斜率存在,根据韦达定理和中点坐标公式,根据![]() ,得出点
,得出点![]() 在线段
在线段![]() 的中垂线上,求得
的中垂线上,求得![]() 的值,即可求出直线方程
的值,即可求出直线方程
(1)依题意:![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
由 ,消
,消![]() 可得
可得![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
故抛物线![]() 的方程为
的方程为![]() .
.
(2)若经过![]() 的直线的斜率不存在,此时直线与抛物线交于
的直线的斜率不存在,此时直线与抛物线交于![]() ,则
,则![]() 关于
关于![]() 轴对称,满足
轴对称,满足![]() ,即直线
,即直线![]() 满足题意.
满足题意.
若经过![]() 的直线的斜率存在,设它为
的直线的斜率存在,设它为![]() ,则
,则![]() .
.
由![]() ,消
,消![]() 可得
可得![]()
设![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴点
,∴点![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
即线段![]() 的中垂线为:
的中垂线为:![]() ,
,
即![]() ,即
,即![]()
所以直线![]() 的方程为
的方程为![]() 即
即![]() .
.
故直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
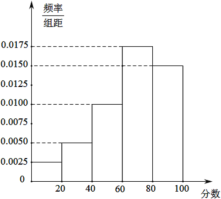
【题目】[2018·临川一中]海盗船是一种绕水平轴往复摆动的游乐项目,因其外形仿照古代海盗船而得名.现有甲、乙两游乐场统计了一天6个时间点参与海盗船游玩的游客数量,具体数据如表:
时间点 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
甲游乐场 | 10 | 3 | 12 | 6 | 12 | 20 |
乙游乐场 | 13 | 4 | 3 | 2 | 6 | 19 |
(1)从所给6个时间点中任选一个,求参与海盗船游玩的游客数量甲游乐场比乙游乐场少的概率;
(2)记甲、乙两游乐场6个时间点参与海盗船游玩的游客数量分别为![]() ,
,![]() (
(![]() ),现从该6个时间点中任取2个,求恰有1个时间点满足
),现从该6个时间点中任取2个,求恰有1个时间点满足![]() 的概率.
的概率.