题目内容

7．已知正方体ABCD-A1B1C1D1中，点P为线段DD1上任意一点，则在正方体的所有棱中与平面ABP平行的共有2或3或4条．

分析 由题意，画出图形，根据正方体中各棱与各面的关系进行判断．

解答 解：如图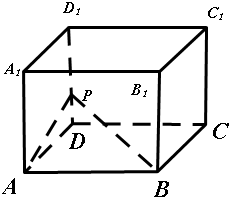
当P与D重合时，平面ABP与底面ABCD重合，
在正方体的所有棱中与平面ABP平行的共有A1B1，C1D1，A1D1，B1C1共有4条；
当P与D1重合时，平面ABP为对角面ABC1D1，在正方体的所有棱中与平面ABP平行的共有CD，A1B1共有2条；
当P在线段DD1之间时（不与端点D，D1重合），在正方体的所有棱中与平面ABP平行的共有A1B1，C1D1，CD共有3条；
综上在正方体的所有棱中与平面ABP平行的共有2，3，4，条；
故答案为：2或3或4．

点评 本题考查了正方体中的线面平行的判断；特别考虑P的特殊位置．

练习册系列答案
相关题目
8．过双曲线x2-y2=4上任意一点M作它的一条渐近线的垂线段，垂足为N，O是坐标原点，则△OMN的面积是1．
18．长方体ABCD-A1B1C1D1中，AA1=$\sqrt{2}$，AB=BC=2，O是底面对角线的交点．
（1）求证：A1O⊥平面BC1D；
（2）求三棱锥A1-DBC1的体积．
15．两条直线都与一个平面平行，则这两条直线的位置关系是（　　）
A．异面B．相交
C．可能共面，也可能异面D．平行
2．正方体ABCD-A1B1C1D1中，与棱AB异面的棱有（　　）
A．2条B．4条C．6条D．8条
12．如图，在四棱锥P-ABCD中，ABCD是正方形，PD⊥平面ABCD，PD=AD=2，E，F，G分别是PC，PD，BC的中点．
（1）求四棱锥P-ABCD的体积；
（2）求证：平面PAB∥平面EFG；
（3）在线段PB上确定一点M，使PC⊥平面ADM，
并给出证明．
19．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD的中点，且AB=2，∠BAD=60°．
（1）求证：OM∥平面PAB；
（2）求证：平面PBD⊥平面PAC；
（3）当三棱锥M-BCD的体积等于$\frac{\sqrt{3}}{4}$时，求PB的长．
16．已知函数f（x）=$\frac{ax+b}{{x}^{2}+c}$是定义在R上的奇函数，且当x=1时，f（x）取最大值1．
（1）求出a，b，c的值并写出f（x）的解析式；
（2）若x1=$\frac{1}{2}$，xn+1=f（xn），求证：$\frac{（{x}_{1}-{x}_{2}）^{2}}{{x}_{1}{x}_{2}}$+$\frac{（{x}_{2}-{x}_{3}）^{2}}{{x}_{2}{x}_{3}}$+…+$\frac{（{x}_{n}-{x}_{n+1}）^{2}}{{x}_{n}{x}_{n+1}}$$＜\frac{5}{16}$；
（3）若x1∈（0，1），xn+1=f（xn），试比较xn+1与xn的大小并证明．
17．如图，四棱锥P-ABCD中，PD⊥平面ABCD，AB∥DC，AD⊥DC，且CD=2，AB=AD=1，∠BCD=45°
（1）若点M是PD的中点，证明：AM∥平面PBC
（2）若△PBC的面积为$\sqrt{2}$，求二面角B-PC-D的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网