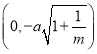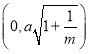题目内容
【题目】已知点F为抛物线C:y2=4x的焦点,过点F作斜率为k的直线l与抛物线交于A,B两点,与准线交于点P,设点D为抛物线准线与x轴的交点.
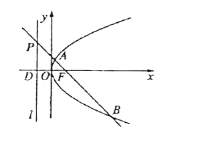
(1)若k=﹣1,求△DAB的面积;
(2)若![]() λ
λ![]() ,
,![]() μ
μ![]() ,证明:λ+μ为定值.
,证明:λ+μ为定值.
【答案】(1)4![]() (2)证明见解析,定值为0
(2)证明见解析,定值为0
【解析】
(1)由直线与抛物线联立得![]() ,根据
,根据![]() ,求得点
,求得点![]() 到直线
到直线![]() 的距离,进而求得三角形的面积,得到答案;
的距离,进而求得三角形的面积,得到答案;
(2)设![]() ,联立方程组,求得
,联立方程组,求得![]() ,结合
,结合![]() λ
λ![]() ,
,![]() μ
μ![]() ,得到λ
,得到λ![]() ,
,![]() ,进而求得
,进而求得![]() 为定值,得到答案.
为定值,得到答案.
(1)由F的坐标分别为(1,0),直线PF的斜率为1,
所以直线PF的方程为y=﹣(x﹣1),
设A,B两点的坐标分别为(x1,y1),(x2,y2),
由直线与抛物线联立得x2﹣6x+1=0,
所以x1+x2=6,x1x2=1.
于是|AB|=x1+x2+2=8.
点D到直线x+y﹣1=0的距离d![]() ,
,
所以S![]() 4
4![]() ;
;
(2)证明:设直线l:y=k(x﹣1).则P(﹣1,﹣2k),
联立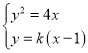 可得ky2﹣4y﹣4k=0,
可得ky2﹣4y﹣4k=0,
![]() ,
,
∵![]() λ
λ![]() ,
,![]() μ
μ![]() ,
,
所以(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,﹣2k﹣y1)=μ(x2+1,y2+2k),
∴λ![]() ,
,![]() .
.
∴λ+μ![]() (定值).
(定值).

练习册系列答案
相关题目