题目内容
[2013·重庆高考]已知函数f(x)=ax3+bsinx+4(a,b∈R),f(lg(log210))=5,则f(lg(lg2))=( )
| A.-5 | B.-1 | C.3 | D.4 |
C
∵f(x)=ax3+bsinx+4, ①
∴f(-x)=a(-x)3+bsin(-x)+4,
即f(-x)=-ax3-bsinx+4, ②
①+②得f(x)+f(-x)=8, ③
又∵lg(log210)=lg(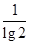 )=lg(lg2)-1=-lg(lg2),
)=lg(lg2)-1=-lg(lg2),
∴f(lg(log210))=f(-lg(lg2))=5,
又由③式知
f(-lg(lg2))+f(lg(lg2))=8,
∴5+f(lg(lg2))=8,
∴f(lg(lg2))=3.故选C.
∴f(-x)=a(-x)3+bsin(-x)+4,
即f(-x)=-ax3-bsinx+4, ②
①+②得f(x)+f(-x)=8, ③
又∵lg(log210)=lg(
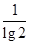 )=lg(lg2)-1=-lg(lg2),
)=lg(lg2)-1=-lg(lg2),∴f(lg(log210))=f(-lg(lg2))=5,
又由③式知
f(-lg(lg2))+f(lg(lg2))=8,
∴5+f(lg(lg2))=8,
∴f(lg(lg2))=3.故选C.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 是R上的偶函数,若将
是R上的偶函数,若将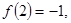 则
则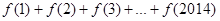 =( )
=( )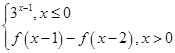 ,则f(2 016)=________.
,则f(2 016)=________.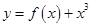 为偶函数,且
为偶函数,且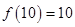 ,若函数
,若函数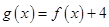 ,则
,则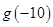
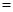 .
.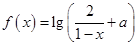 是奇函数,则使f(x)<0的x的取值范围是( ).
是奇函数,则使f(x)<0的x的取值范围是( ).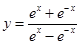 的图像大致为( ).
的图像大致为( ).