题目内容
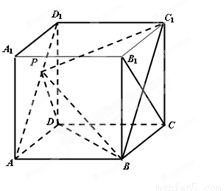
(本题满分14分)如图,在棱长为的正方体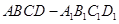 中,
中,
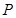 为线段
为线段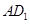 上的点,且满足
上的点,且满足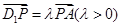 .
.
(Ⅰ)当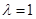 时,求证:平面
时,求证:平面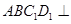 平面
平面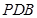 ;
;
(Ⅱ)试证无论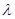 为何值,三棱锥
为何值,三棱锥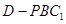 的体积恒为定值;
的体积恒为定值;
 (Ⅲ)求异面直线
(Ⅲ)求异面直线 与
与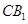 所成的角的余弦值.
所成的角的余弦值.
【答案】
方法一、证明:(Ⅰ)∵正方体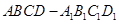 中,
中,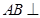 面
面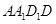 ,
,
又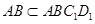 ∴平面
∴平面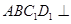 平面
平面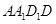 , ∵
, ∵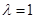 时,
时,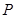 为
为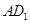 的中点,∴
的中点,∴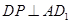 ,
又∵平面
,
又∵平面 平面
平面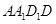
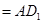 ,∴
,∴ 平面
平面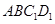 ,
,
又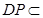 平面
平面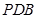 ,∴平面
,∴平面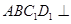 平面
平面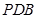 .……………5分
.……………5分
(Ⅱ)∵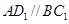 ,
,
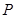 为线段
为线段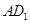 上的点,
上的点,
∴三角形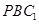 的面积为定值,即
的面积为定值,即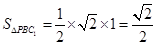 ,
,
又∵ 平面
平面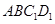 ∴点
∴点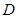 到平面
到平面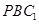 的距离为定值,
的距离为定值,
即 , ∴三棱锥
, ∴三棱锥 的体积为定值,
的体积为定值,
即 .
.
也即无论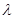 为何值,三棱锥
为何值,三棱锥 的体积恒为定值
的体积恒为定值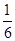 ; ……………10分
; ……………10分
(Ⅲ)∵由(Ⅰ)易知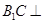 平面
平面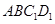 ,又
,又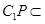 平面
平面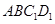 ,∴
,∴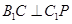 ,
即异面直线
,
即异面直线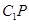 与
与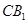 所成的角为定值
所成的角为定值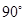 ,从而其余弦值为
,从而其余弦值为 .
……………14分
.
……………14分
方法二、如图,以点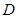 为坐标原点,建立如图所示的坐标系.
为坐标原点,建立如图所示的坐标系.
(Ⅰ)当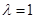 时,即点
时,即点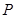 为线段
为线段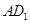 的中点,则
的中点,则 ,又
,又 、
、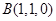

∴ ,
,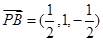 ,设平面
,设平面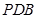 的法向量为
的法向量为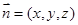 ……1分
……1分
则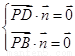 ,即
,即 ,令
,令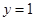 ,
,
解得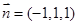 ,……2分
,……2分
又∵点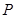 为线段
为线段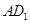 的中点,∴
的中点,∴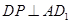 ,
,
∴ 平面
平面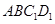 ,
,
∴平面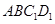 的法向量为
的法向量为 ,
………3分
,
………3分
∵ ,
,
∴平面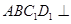 平面
平面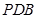 ,
………………………6分
,
………………………6分
(Ⅱ)略; ………………………10分
(Ⅲ)∵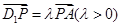 ,∴
,∴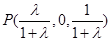 , ………………………11分
, ………………………11分
又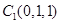 、
、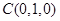 、
、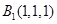 ,∴
,∴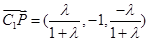 ,
, …12分
…12分
∵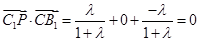 ……………………13分
……………………13分
∴不管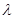 取值多少,都有
取值多少,都有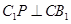 ,
,
即异面直线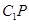 与
与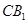 所成的角的余弦值为0.
……………14分
所成的角的余弦值为0.
……………14分
【解析】略

练习册系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;