Question

9．在△ABC中，O为中线BD上的一个动点，若BD=6，则$\overrightarrow{OB}•（{\overrightarrow{OA}+\overrightarrow{OC}}）$的最小值是（　　）

• A． 0
• B． -9
• C． -18
• D． -24

Answer 1

分析 O在中线BD上，从而分O和B或D重合，O在B与D之间两种情况进行求解：而对于第一种情况容易求出$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）=0$，对于第二种情况，根据向量加法的平行四边形法则即可得到$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）$=$-2|\overrightarrow{OB}||\overrightarrow{OD}|$，而$|\overrightarrow{OB}|+|\overrightarrow{OD}|=6$，且$|\overrightarrow{OB}|，|\overrightarrow{OD}|＞0$，从而根据基本不等式即可得到$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）≥-18$，从而便可求出$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）$的最小值．

解答 解：如图，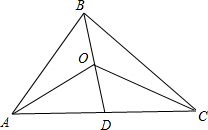
（1）当O和B或D重合时，显然$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）=0$；
（2）当O在B，D之间时，$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）=2\overrightarrow{OB}•\overrightarrow{OD}$=$-2|\overrightarrow{OB}||\overrightarrow{OD}|$；
而$|\overrightarrow{OB}|＞0，|\overrightarrow{OD}|＞0$，且$|\overrightarrow{OB}|+|\overrightarrow{OD}|=6$；
∴$|\overrightarrow{OB}||\overrightarrow{OD}|≤（\frac{|\overrightarrow{OB}|+|\overrightarrow{OD}|}{2}）^{2}=9$；
∴$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）≥-18$，当且仅当$|\overrightarrow{OB}|=|\overrightarrow{OD}|$，即O为中线BD中点时取“=”；
∴$\overrightarrow{OB}•（\overrightarrow{OA}+\overrightarrow{OC}）$的最小值为-18．
故选C．

点评 考查向量加法的平行四边形法则，数量积的计算公式，基本不等式，注意应用基本不等式所具备的条件．