题目内容
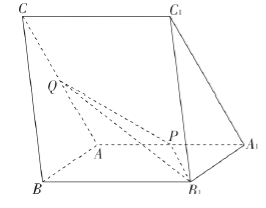
【题目】【2017黑龙江大庆实验中学仿真模拟】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
【答案】见解析
【解析】

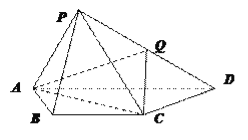
(Ⅰ)证明 如图所示,取PA的中点N,连接QN,
BN.在△PAD中,PN=NA,PQ=QD,
所以QN∥AD,且QN=![]() AD.
AD.
在△APD中,PA=2,PD=2![]() ,PA⊥PD,
,PA⊥PD,
所以AD=![]() =4,而BC=2,所以BC=
=4,而BC=2,所以BC=![]() AD.
AD.
又BC∥AD,所以QN∥BC,且QN=BC,
故四边形BCQN为平行四边形,所以BN∥CQ.
又BN平面PAB,且CQ![]() 平面PAB, 所以CQ∥平面PAB.
平面PAB, 所以CQ∥平面PAB.
(Ⅱ)如图,取AD的中点M,连接BM;取BM的中点O,连接BO、PO.
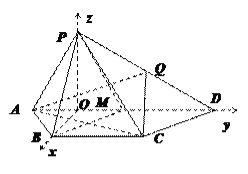
由(1)知PA=AM=PM=2,
所以△APM为等边三角形,
所以PO⊥AM. 同理BO⊥AM.
因为平面PAD⊥平面ABCD,所以PO⊥BO.
如图,以O为坐标原点,分别以OB,OD,OP所在直线为x轴,y轴,z轴建立空间直角坐标系,则O(0,0,0),D(0,3,0),A(0,-1,0),B(![]() ,0,0),P(0,0,
,0,0),P(0,0,![]() ),C(
),C(![]() ,2,0),
,2,0),
则![]() =(
=(![]() ,3,0).
,3,0).
因为Q为DP的中点,故Q![]() ,所以
,所以![]() =
=![]() .
.
设平面AQC的法向量为m=(x,y,z),
则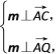 可得
可得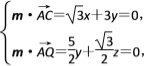
令y=-![]() ,则x=3,z=5. 故平面AQC的一个法向量为m=(3,-
,则x=3,z=5. 故平面AQC的一个法向量为m=(3,-![]() ,5).
,5).
设直线PD与平面AQC所成角为θ.
则sinθ= |cos〈![]() ,m〉|==
,m〉|==![]() .
.
从而可知直线PD与平面AQC所成角正弦值为![]() .
.

练习册系列答案
相关题目