题目内容
1.函数f(x)=$\frac{x}{mx+n}$(m,n为常数,且m≠0)满足f(1)=$\frac{1}{2}$,f(x)=x有唯一解,则f(x)=( )| A. | $\frac{x}{x+1}$ | B. | $\frac{x}{3x-1}$ | C. | $\frac{2x}{3x+1}$ | D. | $\frac{2x}{3x-1}$ |
分析 由f(1)=$\frac{1}{2}$可得m+n=2,由f(x)=x有唯一解化简可得1-n=0,从而解得.
解答 解:由题意,f(1)=$\frac{1}{m+n}$=$\frac{1}{2}$,
∴m+n=2,
f(x)-x=$\frac{x}{mx+n}$-x=x•$\frac{1-mx-n}{mx+n}$=0,
∵f(x)=x有唯一解,
∴1-n=0,
∴n=1,m=1;
故f(x)=$\frac{x}{x+1}$;
故选A.
点评 本题考查了函数与方程的关系应用及分式方程的解法,属于中档题.

练习册系列答案
相关题目
11.将4名教师分配到3所学校任教,每所学校至少1名教师,则不同的分配方案种数是( )
| A. | C43 | B. | A43 | C. | C42A33 | D. | 34 |
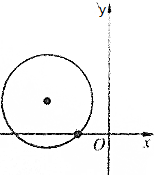 如图,定圆半径为a,圆心为(b,c),则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.
如图,定圆半径为a,圆心为(b,c),则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.