题目内容
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分,且比赛结束.已知射手甲在100m处击中目标的概率为 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(1)求射手甲在这次射击比赛中命中目标的概率;
(2)求射手甲在这次射击比赛中得分的数学期望.
 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.(1)求射手甲在这次射击比赛中命中目标的概率;
(2)求射手甲在这次射击比赛中得分的数学期望.
(1)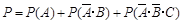
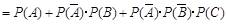
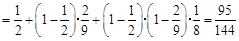 .
.
(2)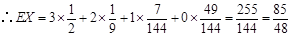 .
.
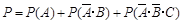
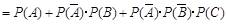
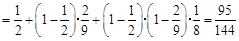 .
.(2)
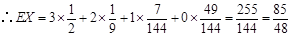 .
.本试题主要是考查了概率、独立事件概率的乘法公式,以及对立事件的运用。
(1)根据已知条件,设出所求解的事件,然后利用独立事件的乘法公式分情况讨论,结合互斥事件的加法公式得到结论。
(2)根据随机变量射手甲得分为X,根据得分的情况分别求解概率值,得到分布列和期望值。
解:记第一、二、三次射击命中目标分别为事件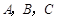 ,三次都未击中目标为事件D,依题意
,三次都未击中目标为事件D,依题意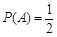 ,设在
,设在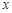 m处击中目标的概率为
m处击中目标的概率为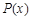 ,则
,则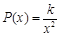 ,且
,且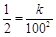 ,
,
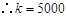 ,即
,即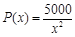 , 。。。。。。。。。。
, 。。。。。。。。。。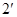
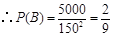 ,
,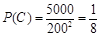 ,
,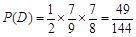 .。。。。。。。。。。。。
.。。。。。。。。。。。。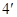
(1) 由于各次射击都是相互独立的,
∴该射手在三次射击中击中目标的概率
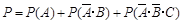
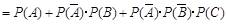
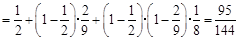 . 。。。。。
. 。。。。。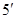
(2)依题意,设射手甲得分为X,则 ,
,
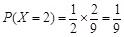 ,
,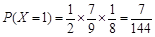 ,
,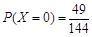 ,。。。。。。。
,。。。。。。。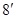
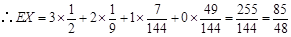 . 。。。。。。。。。。。。。。。。。。
. 。。。。。。。。。。。。。。。。。。
(1)根据已知条件,设出所求解的事件,然后利用独立事件的乘法公式分情况讨论,结合互斥事件的加法公式得到结论。
(2)根据随机变量射手甲得分为X,根据得分的情况分别求解概率值,得到分布列和期望值。
解:记第一、二、三次射击命中目标分别为事件
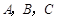 ,三次都未击中目标为事件D,依题意
,三次都未击中目标为事件D,依题意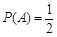 ,设在
,设在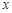 m处击中目标的概率为
m处击中目标的概率为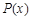 ,则
,则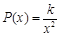 ,且
,且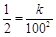 ,
,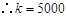 ,即
,即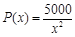 , 。。。。。。。。。。
, 。。。。。。。。。。
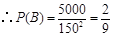 ,
,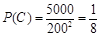 ,
,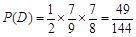 .。。。。。。。。。。。。
.。。。。。。。。。。。。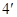
(1) 由于各次射击都是相互独立的,
∴该射手在三次射击中击中目标的概率
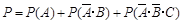
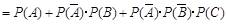
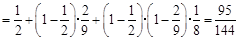 . 。。。。。
. 。。。。。
(2)依题意,设射手甲得分为X,则
 ,
,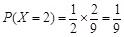 ,
,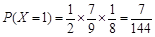 ,
,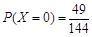 ,。。。。。。。
,。。。。。。。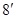
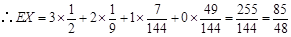 . 。。。。。。。。。。。。。。。。。。
. 。。。。。。。。。。。。。。。。。。

练习册系列答案
相关题目
 . 当
. 当 . 求
. 求 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.  :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质 ,求
,求 .
. 表示4名乘客在第4层下电梯的人数,则
表示4名乘客在第4层下电梯的人数,则 ,求
,求 ,二等品率为
,二等品率为 ;乙产品的一等品率为
;乙产品的一等品率为 ,二等品率为
,二等品率为 .生产
.生产 件甲产品,若是一等品,则获利
件甲产品,若是一等品,则获利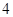 万元,若是二等品,则亏损
万元,若是二等品,则亏损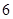 万元,若是二等品,则亏损
万元,若是二等品,则亏损 万
万 (单位:万元),求
(单位:万元),求 万元的概率.
万元的概率.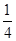 ,8∶20发出的概率为
,8∶20发出的概率为 ,8∶40发出的概率为
,8∶40发出的概率为 的分布列和数学期望。
的分布列和数学期望。 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 。
。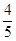 ,第二、第三种
,第二、第三种 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
 的值;
的值; .
.