题目内容
(本题满分14分)
某学校某班文娱小组的每位组员唱歌、跳舞至少会一项,已知已知会唱歌的有2人,会跳舞听有5人,现从中选2人。设 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 。
。
(1)请你判断该班文娱小组的人数并说明理由;
(2)求 的分布列与数学期望。
的分布列与数学期望。
某学校某班文娱小组的每位组员唱歌、跳舞至少会一项,已知已知会唱歌的有2人,会跳舞听有5人,现从中选2人。设
 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 。
。(1)请你判断该班文娱小组的人数并说明理由;
(2)求
 的分布列与数学期望。
的分布列与数学期望。解法一:(1)既会唱歌又会跳舞的有2人,且文娱队中共有5人
(2)
 | 0 | 1 | 2 |
| P | 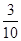 | 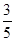 | 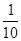 |
∴
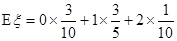 =
=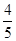 .
. 解法一:(1)设既会唱歌又会跳舞的有x人,那么由题意可知:
只会唱歌的有(2-x)人,只会跳舞的有(5-x)人,
文娱队中共有(7-x)人,那么只会一项的人数是(7-2 x)人.--------------------------(3分)
显然x可以取得的值只有0,1,2
① 当x=0时,
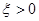 为不可能事件,显然不符合题意-------------------------------(4分)
为不可能事件,显然不符合题意-------------------------------(4分)② 当x=1时,
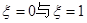 是对立事件,且
是对立事件,且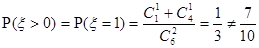
所以x=1时不符合题意---------------------------------------------------------------(6分)
③当x=2时,
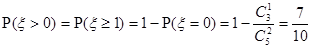 符合题意。----(8分)
符合题意。----(8分)综上可知道:既会唱歌又会跳舞的有2人,且文娱队中共有5人-----------------(9分)
(2)
 的可能取值为0,1,2 -----------------------------------------------------(10分)
的可能取值为0,1,2 -----------------------------------------------------(10分)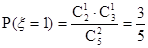 ,------------------------------------------------(11分)
,------------------------------------------------(11分) ,--------------------------------------------------(12分)
,--------------------------------------------------(12分) | 0 | 1 | 2 |
| P | 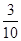 | 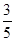 | 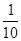 |
∴
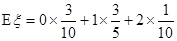 =
=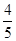 . -------------------------------(14分)
. -------------------------------(14分)如果按照下列解法最多给10分
解法二:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是(7-2 x)人.-------------------------------------------------(2分)
(I)∵
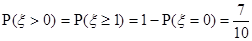 ,∴
,∴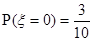 .……………(3分)
.……………(3分)即
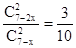 .∴
.∴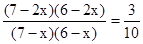 .∴x=2.
.∴x=2.故文娱队共有5人.……………………………………(5分)
(II)
 的可能取值为0,1,2 -----------------------------------------------------(6分)
的可能取值为0,1,2 -----------------------------------------------------(6分)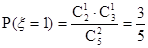 ,---------------------------------------------------(7分)
,---------------------------------------------------(7分) ,----------------------------------------------------(8分)
,----------------------------------------------------(8分) | 0 | 1 | 2 |
| P | 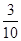 | 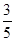 | 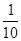 |
∴
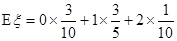 =
=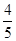 . -------------------------------(10分)
. -------------------------------(10分) 
练习册系列答案
相关题目
 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的. ,求随机变量
,求随机变量 .(8分)
.(8分) ,k=1,2,3,则D(3X +5)等于 ( )
,k=1,2,3,则D(3X +5)等于 ( ) .
. ,一等品率提高为
,一等品率提高为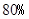 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?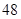 名同学,一次考试后的数学成绩服从正态分布
名同学,一次考试后的数学成绩服从正态分布 ,则理论上
,则理论上 分到
分到  分的人数是 ( )
分的人数是 ( ) 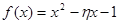 在区间
在区间 ,
, 内有零点”的事件为
内有零点”的事件为 ,求
,求 ;
;