题目内容
(本小题12分)为了丰富学生的课余生活,促进校园文化建设,我校高二年级通过预赛选出了6个班(含甲、乙)进行经典美文颂读比赛决赛.决赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)决赛中甲、乙两班之间的班级数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)决赛中甲、乙两班之间的班级数记为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.(1) ;
;
(2)随机变量 的分布列为:
的分布列为:
因此 ,
,
 ;
;(2)随机变量
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 4 |
 | 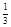 |  |  |  |  |
 ,
,本试题主要是考查了古典概型和分布列以及期望值的运用。
(1)由于设“甲、乙两班恰好在前两位出场”为事件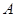 ,则
,则
所以 甲、乙两班恰好在前两位出场的概率为
(2)根据题意可知随机变量 的可能取值为
的可能取值为 .,那么各个取值的概率值得到,从而得到分布列和期望值。
.,那么各个取值的概率值得到,从而得到分布列和期望值。
解:(1)设“甲、乙两班恰好在前两位出场”为事件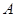 ,则
,则
所以 甲、乙两班恰好在前两位出场的概率为 ………………………………4分
………………………………4分
(2)随机变量 的可能取值为
的可能取值为 .
.
 ,
,  ,
,  ,
,

 ……………………10分
……………………10分
随机变量 的分布列为:
的分布列为:
因此 ,
,
(1)由于设“甲、乙两班恰好在前两位出场”为事件
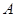 ,则
,则
所以 甲、乙两班恰好在前两位出场的概率为

(2)根据题意可知随机变量
 的可能取值为
的可能取值为 .,那么各个取值的概率值得到,从而得到分布列和期望值。
.,那么各个取值的概率值得到,从而得到分布列和期望值。解:(1)设“甲、乙两班恰好在前两位出场”为事件
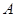 ,则
,则
所以 甲、乙两班恰好在前两位出场的概率为
 ………………………………4分
………………………………4分(2)随机变量
 的可能取值为
的可能取值为 .
.  ,
,  ,
,  ,
,
 ……………………10分
……………………10分随机变量
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 4 |
 | 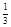 |  |  |  |  |
 ,
,
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min. 的分布列及期望.
的分布列及期望.
 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的. 局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为
局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立.现知前
,各局比赛结果相互独立.现知前 局中,甲、乙各胜
局中,甲、乙各胜 局,设
局,设 表示从第
表示从第 ,k=1,2,3,则D(3X +5)等于 ( )
,k=1,2,3,则D(3X +5)等于 ( ) ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数 的分布列与期望
的分布列与期望