题目内容
【题目】已知不等式 
＞x的解集为（﹣∞，m）．
（Ⅰ）求实数m的值；
（Ⅱ）若关于x的方程|x﹣n|+|x+ 
|=m（n＞0）有解，求实数n的值．
【答案】解：（Ⅰ）由题意得： 
＞x， 故|x+3|﹣2x﹣1＞0，
故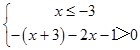 
或 
，
解得：x＜2，故m=2；
（Ⅱ）由题意得|x﹣n|+|x+ 
|=2有解，
∵|x﹣n|+|x+ |≥|（x﹣n）﹣（x+ ）|=|n+ |=n+ ≥2，
当且仅当n=1时”=“成立，
故n=1
【解析】（Ⅰ）根据x的范围得到关于x的不等式组，解出即可；（Ⅱ）根据绝对值不等式的性质得到关于n的不等式，解出即可．
【考点精析】认真审题，首先需要了解绝对值不等式的解法(含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号)．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
