题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设曲线![]() ,点
,点![]() ,
,![]() 为该曲线上不同的两点.求证:当
为该曲线上不同的两点.求证:当![]() 时,直线
时,直线![]() 的斜率大于-1.
的斜率大于-1.
【答案】(Ⅰ)答案见解析;(Ⅱ)![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】分析:(Ⅰ)对函数进行求导得![]() ,对
,对![]() 分为
分为![]() 和
和![]() 两种情形,讨论导数与0的关系,即可得单调性;(Ⅱ)利用分离参数的思想,原不等式等价于
两种情形,讨论导数与0的关系,即可得单调性;(Ⅱ)利用分离参数的思想,原不等式等价于![]() ,
,![]() 成立,令
成立,令![]() ,利用导数求出其最小值即可;(Ⅲ)不妨设
,利用导数求出其最小值即可;(Ⅲ)不妨设![]() 且
且![]() ,要证明直线AB斜率大于
,要证明直线AB斜率大于![]() ,即证
,即证![]() ,
,![]() ,利用导数证明其单调递增即可.
,利用导数证明其单调递增即可.
详解:(Ⅰ)![]()
![]() ,
,
若![]() ,
,![]() ,
,
无单调递增区间.
若![]() ,由
,由![]() ,
,
当![]() ,
,![]() ;
;
当![]() ,
,![]() .
.
综上所述:当![]() 时,
时,![]() ,无单调递增区间;
,无单调递增区间;
当![]() 时,
时,![]() ,
,![]() .
.
(Ⅱ)当![]() ,
,![]() 时
时
![]() ,
,
因为![]() ,
,![]() 成立,
成立,
即![]() ,
,![]() 成立,
成立,
即![]() ,
,![]() 成立,
成立,
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故当![]() 时,
时,![]() 有极小值
有极小值![]() ,此极小值即为最小值,
,此极小值即为最小值,
因为![]() ,
,![]() 成立,所以
成立,所以![]() ,因此
,因此![]() ,
,
即![]() 的取值范围为
的取值范围为![]() .
.
(Ⅲ)不妨设![]() 且
且![]() ,要证明直线AB斜率大于
,要证明直线AB斜率大于![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
由已知![]() ,其中
,其中![]() ,
,![]() ,
,
设![]() ,
,
则![]() ,
,
![]() ,因此当
,因此当![]() 时,
时,![]() ,
,
即![]() ,所以原命题得证.
,所以原命题得证.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
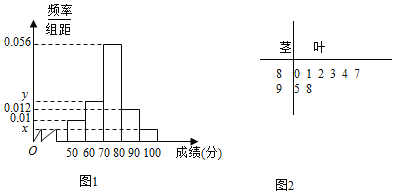
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
【题目】(本小题满分12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)在本次训练中,从两班中分别任选一个同学,比较两人的投中次数,求甲班同学投中次数高于乙班同学投中次数的概率.