题目内容
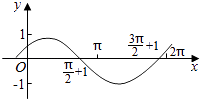
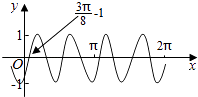
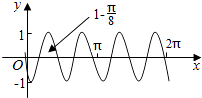
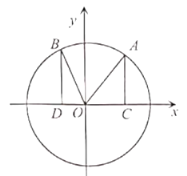
【题目】如图,在平面直角坐标系![]() 中,单位圆
中,单位圆![]() 上存在两点
上存在两点![]() ,满足
,满足![]() 均与
均与![]() 轴垂直,设
轴垂直,设![]() 与
与![]() 的面积之和记为
的面积之和记为![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若对任意的
若对任意的![]() ,存在
,存在![]() ,使得
,使得![]() 成立,且实数
成立,且实数![]() 使得数列
使得数列![]() 为递增数列,其中
为递增数列,其中![]() 求实数
求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)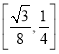
【解析】
(1)运用三角形的面积公式和三角函数的和差公式,以及特殊角的函数值,可得所求角;
(2)由正弦函数的值域可得![]() 的最大值,再由基本不等式可得
的最大值,再由基本不等式可得![]() 的最大值,可得
的最大值,可得![]() 的范围,再由数列的单调性,讨论
的范围,再由数列的单调性,讨论![]() 的范围,即可得到
的范围,即可得到![]() 的取值范围.
的取值范围.
![]() 依题意,可得
依题意,可得
![]()
![]()
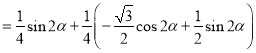
![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() .
.
![]() 由
由![]() 得
得![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,
,
(当且仅当![]() 时,等号成立)
时,等号成立)
又因为对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
因为数列![]() 为递增数列,且
为递增数列,且![]() ,
,
所以![]() ,从而
,从而![]() ,
,
又![]() ,所以
,所以![]() ,
,
从而![]() ,
,
又![]() ,
,
①当![]() 时,
时,![]() ,从而
,从而![]() ,
,
此时![]() 与
与![]() 同号,
同号,
又![]() ,即
,即![]() ,
,
②当![]() 时,由于
时,由于![]() 趋向于正无穷大时,
趋向于正无穷大时,![]() 与
与![]() 趋向于相等,从而
趋向于相等,从而![]() 与
与![]() 趋向于相等,即存在正整数
趋向于相等,即存在正整数![]() ,使
,使![]() ,从而
,从而![]() ,
,
此时![]() 与
与![]() 异号,与数列
异号,与数列![]() 为递增数列矛盾,
为递增数列矛盾,
综上,实数![]() 的取值范围为
的取值范围为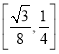 .
.

练习册系列答案
相关题目