Question

【题目】已知函数.

（Ⅰ）当时,求曲线在点处的切线方程;

（Ⅱ）若函数在上单调递减,试求的取值范围;

（Ⅲ）若函数的最小值为,试求的值.

Answer 1

【答案】（Ⅰ）.（Ⅱ）.（Ⅲ）.

【解析】试题分析：（Ⅰ）利用导数求出处的切线斜率，根据点斜式写出切线方程；（Ⅱ）函数在上单调递减，即当时， 恒成立，等价于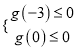，即可求出的取值范围；（Ⅲ）根据函数的单调性，得出函数的最小值只能在处取得，从而求得的值.

试题解析：（Ⅰ）当时,由得: .

又∵

∴.

∴切线方程为: ,即.

（Ⅱ）∵函数在上单调递减

∴当时, 恒成立,即当时, 恒成立.

∵函数的对称轴为,并且开口向上,

∴当时,函数单调递减;当时,函数单调递增.

∴“当时, 恒成立”必须满足: 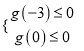,解得.

∴, 的取值范围是.

（Ⅲ）设.

①当时, , 恒成立,

∴恒成立, 在上单调递增,函数没有最小值.

②当时, .

令得: ，解得.

∴当时, , 单调递增;

当时, , 单调递减;

当时, , 单调递增.

∴当时, 取得极大值;

当时, 取得极小值.

∴当时, ,

∴,则,

又∵函数的最小值为,

∴函数的最小值只能在处取得,则,

∴,即,解得.