题目内容
【题目】设数列{an}满足:①a1=1;②所有项an∈N*;③1=a1<a2<…<an<an+1<….设集合Am={n|an≤m,m∈N*),将集合Am中的元素的最大值记为bm,即bm是数列{an}中满足不等式an≤m的所有项的项数的最大值.我们称数列{bn}为数列{an}的伴随数列.
例如,数列1,3,5的伴随数列为1,1,2,2,3.
(I)若数列{an}的伴随数列为1,1,2,2,2,3,3,3,3……,请写出数列{an};
(II)设an=4n-1,求数列{an}的伴随数列{bn}的前50项之和;
(III)若数列{an}的前n项和![]() (其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
(其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
【答案】(I)1,3,6 (II)Tm=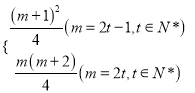
【解析】试题分析:(1)直接根据伴随数列的定义可得出数列![]() 的前三项;(2)当
的前三项;(2)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]()
![]() ,(3)讨论两种情况,当
,(3)讨论两种情况,当![]() 时;
时; ![]() ;当
;当![]() 时,
时, ![]() .
.
试题解析:(I)1,3,6 (II)由an=4n-1≤m,得n≤l+log4m(m∈N*)
当1≤m≤3,m∈N*时,b1=b2=b3=1
当4≤m≤15,m∈N*时,b4=b5=…=b15=2
当16≤m≤50,m∈N*时,b16=b17=…=b50=3
∴b1+b2+…+b50=1×3+2×12+3×35=132
(III)∵a1=S1=1+c=1 ∴c=0
当n≥2时,an=Sn-Sn-1=2n-1 ∴an=2n-1(n∈N*)
由an=2n-l≤m得,n≤![]() (m∈N*)
(m∈N*)
因为使得an≤m成立的n的最大值为bm,
所以b1=b2=1,b3=b4=2,…,b2t-1=b2t=t(t∈N*)
当m=2t-1(t∈N*)时;
Tm=2·![]() ·(t-1)+t=t2=
·(t-1)+t=t2=![]() (m+1)2
(m+1)2
当m=2t (t∈N*)时;
Tm=2·![]() ·t=t2+t=
·t=t2+t=![]() m(m+2)
m(m+2)
所以Tm=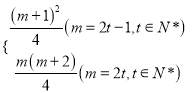

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.