题目内容
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎么变化,总有
怎么变化,总有![]() 为直角,点
为直角,点![]() 坐标为
坐标为![]() 或
或![]() .
.
【解析】试题分析:(1)依题意,![]() ,结合点
,结合点![]() 在椭圆
在椭圆![]() 上及
上及![]() ,即可求得椭圆
,即可求得椭圆![]() 的方程;(2)设
的方程;(2)设![]() ,则
,则![]() ,联立直线与椭圆的方程,求得
,联立直线与椭圆的方程,求得![]() ,
,![]() ,根据
,根据![]() 得
得![]() 所在直线方程,即可分别得到
所在直线方程,即可分别得到![]() 与
与![]() 的坐标,结合
的坐标,结合![]() 为直角,列出等式,即可求解.
为直角,列出等式,即可求解.
试题解析:(1)依题意,![]() .
.
∵点![]() 在
在![]() 上,
上,
∴![]() ,
,
又∵![]()
∴![]() ,
,
∴椭圆方程为![]()
(2)假设存在这样的点![]() ,设
,设![]() ,则
,则![]() ,联立
,联立 ,解得
,解得![]() ,
,
∵![]()
∴![]() 所在直线方程为
所在直线方程为![]() ,
,
∴![]() ,
,
同理可得![]() ,
,![]() ,
,![]() .
.
∴![]() 或
或![]()
∴存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎么变化,总有
怎么变化,总有![]() 为直角,点
为直角,点![]() 坐标为
坐标为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
甲生产线生产的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
乙生产线产生的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
|
频数 | 10 | 15 | 25 | 30 | 20 |
(1)若从乙生产线生产的产品中有放回地随机抽取3件,求至少抽到2件三等品的概率;
(2)若该产品的利润率![]() 与质量指标值
与质量指标值![]() 满足关系:
满足关系: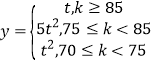 ,其中
,其中![]() ,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.