题目内容
已知函数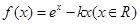
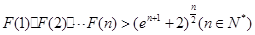 .
.
(Ⅰ)若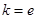 ,试确定函数
,试确定函数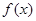 的单调区间;
的单调区间;
(Ⅱ)若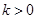 且对任意
且对任意 恒成立,试确定实数
恒成立,试确定实数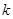 的取值范围;
的取值范围;
(Ⅲ)设函数 ,求证:
,求证: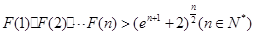 .
.
【答案】
(Ⅰ)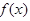 在
在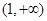 单调递增;在
单调递增;在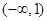 单调递减 4分
单调递减 4分
(Ⅱ)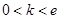 .
.
(Ⅲ)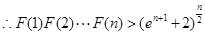 .
.
【解析】
试题分析:(Ⅰ)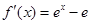 ,令
,令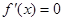 ,解得
,解得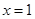
当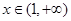 时,
时,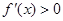 ,
,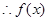 在
在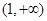 单调递增;
单调递增;
当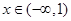 时,
时,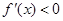 ,
,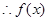 在
在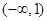 单调递减 4分
单调递减 4分
(Ⅱ)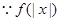 为偶函数,
为偶函数,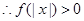 恒成立等价于
恒成立等价于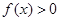 对
对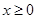 恒成立
恒成立
解法1:当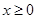 时,
时,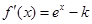 ,令
,令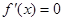 ,解得
,解得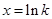
(1)当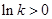 ,即
,即 时,
时,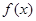 在
在 减,在
减,在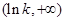 增
增
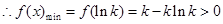 ,解得
,解得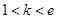 ,
,
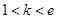
(2)当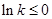 ,即
,即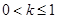 时,
时,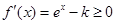 ,
,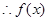 在
在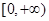 上单调递增,
上单调递增,
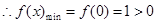 ,符合,
,符合,
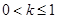
综上,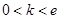 .
9分
.
9分
解法2: 等价于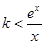 对
对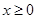 恒成立,
恒成立,
设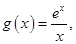 则
则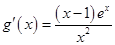 . 当
. 当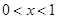 时,
时,  ;当
;当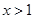 时,
时, 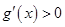 ;
;
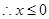 时,
时, 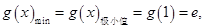
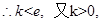
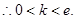
(Ⅲ)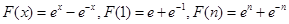
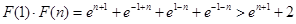
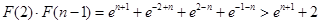
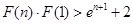
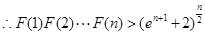 .
14分
.
14分
考点:应用导数研究函数的单调性,证明不等式恒。
点评:难题,本题属于导数应用中的基本问题,在某区间,导数值非负,函数为增函数,导数值非正,函数为减函数。不等式证明问题,往往通过构造函数,转化成了研究函数的最值,使问题得解。本题涉及不等式恒成立问题,通过研究函数的最值,解决了问题。

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|