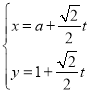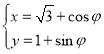题目内容
【题目】已知椭圆C:![]() 的焦距为
的焦距为![]() ,且C过点
,且C过点![]() .
.
(1)求椭圆C的方程;
(2)设![]() 、
、![]() 分别是椭圆C的下顶点和上顶点,P是椭圆上异于
分别是椭圆C的下顶点和上顶点,P是椭圆上异于![]() 、
、![]() 的任意一点,过点P作
的任意一点,过点P作![]() 轴于M,N为线段PM的中点,直线
轴于M,N为线段PM的中点,直线![]() 与直线
与直线![]() 交于点D,E为线段
交于点D,E为线段![]() 的中点,O为坐标原点,则
的中点,O为坐标原点,则![]() 是否为定值,若是,请求出定值;若不是,请说明理由.
是否为定值,若是,请求出定值;若不是,请说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(Ⅰ)由焦距为![]() ,得
,得![]() ,由椭圆过点
,由椭圆过点![]() ,得
,得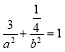 ,再由a2=b2+c2,解得a=2,b=1,由此能求出椭圆C的方程;
,再由a2=b2+c2,解得a=2,b=1,由此能求出椭圆C的方程;
(Ⅱ)设P(x0,y0),x0≠0,则M(0,y0),![]() ,由此能求出直线B2N的方程,令y=﹣1,得
,由此能求出直线B2N的方程,令y=﹣1,得![]() ,由B2(0,﹣1),E为线段B1D的中点,得
,由B2(0,﹣1),E为线段B1D的中点,得![]() ,从而
,从而![]() ,
,![]() ,由此能证明
,由此能证明![]() .
.
(1)由题意各焦距为![]() ,∴
,∴![]() ,又∵椭圆过点
,又∵椭圆过点![]() ,
,
∴代入椭圆方程得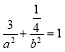 ,∵
,∵![]() ,解得
,解得![]() ,
,![]() ,
,
故所求椭圆C的方程是![]() ;
;
(2)证明:设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∵点P在椭圆C上,![]() ,即
,即![]() ,
,
又![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() ,
,
又![]() ,E为线段
,E为线段![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() ,
,![]() ,
,
因![]()
![]() .
.
∴![]() ,即
,即![]() .
.

练习册系列答案
相关题目