题目内容
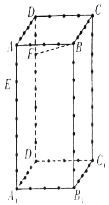
【题目】已知直角△![]() 如图所示,其中
如图所示,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的中点.现沿折痕
边上的中点.现沿折痕![]()
![]() 将
将![]() 翻折,使得
翻折,使得![]() 与平面
与平面![]() 外一点
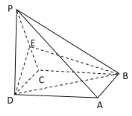
外一点![]() 重合,得到如图(2)所示的几何体.
重合,得到如图(2)所示的几何体.


(1)证明:平面![]() 平面
平面![]() ;
;
(2)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,探究:直线
,探究:直线![]() 与
与![]() 是否平行.若平行,请给出证明,若不平行,请说明理由.
是否平行.若平行,请给出证明,若不平行,请说明理由.
【答案】详见解析
【解析】
试题分析:(1)要证明面面垂直,先证明线面垂直,根据所给的条件,可知![]() ,
,![]() ,这样可知
,这样可知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;(2)要证明线与线平行,可先证明线面平行,根据线面平行的性质定理,可证明线线平行,而根据条件,
;(2)要证明线与线平行,可先证明线面平行,根据线面平行的性质定理,可证明线线平行,而根据条件,![]() ,可证明
,可证明![]() 平面
平面![]() ,这样就可证明
,这样就可证明![]() 平行与交线
平行与交线![]() .
.
试题解析:(1)∵![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
∵![]() 平面
平面![]() ,平面
,平面![]()
![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目
【题目】为了准备里约奥运会的选拔,甲、乙两人进行队内射箭比赛,各射4支箭,两人4次所得环数如下:(最高为10环)
甲 | 6 | 6 | 9 | 9 |
乙 | 7 | 9 |
|
|
(Ⅰ)已知在乙的4支箭中随机选取1支时,此支射中环数小于6环的概率不为零,且在4支箭中,乙的平均环数高于甲的平均环数,求![]() 的值;
的值;
(Ⅱ)如果![]() ,
,![]() ,从甲、乙两人的4次比赛中随机各选取1次,并将其环数分别记为
,从甲、乙两人的4次比赛中随机各选取1次,并将其环数分别记为![]() ,
,![]() ,求
,求![]() 的概率;
的概率;
(Ⅲ)在4次比赛中,若甲、乙两人的平均环数相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)