题目内容
(本小题满分12分)数列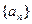 的前n项和为
的前n项和为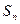 ,
,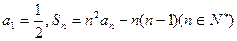
(1)求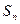 关于n的表达式;
关于n的表达式;
(2)设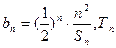 为数列
为数列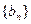 的前n项和,试比较
的前n项和,试比较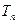 与
与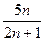 的大小,并加以证明
的大小,并加以证明
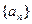 的前n项和为
的前n项和为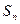 ,
,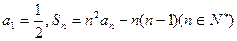
(1)求
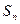 关于n的表达式;
关于n的表达式;(2)设
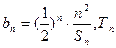 为数列
为数列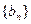 的前n项和,试比较
的前n项和,试比较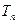 与
与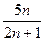 的大小,并加以证明
的大小,并加以证明(1)
(2)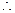 当
当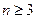 时,有
时,有 证明略
证明略

(2)
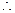 当
当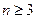 时,有
时,有 证明略
证明略解:(1)当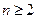 时,
时,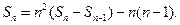 即
即
于是
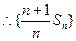 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。
从而 .………………6分
.………………6分
(2) 则
则 ,
, 。…………9分
。…………9分
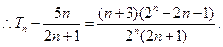 显然:当
显然:当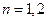 时,有
时,有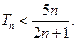
当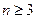 时,
时,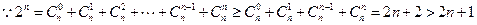
 当
当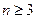 时,有
时,有 …………………..12分
…………………..12分
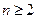 时,
时,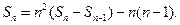 即
即
于是

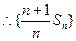 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。从而
 .………………6分
.………………6分(2)
 则
则 ,
, 。…………9分
。…………9分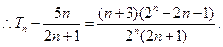 显然:当
显然:当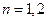 时,有
时,有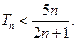
当
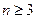 时,
时,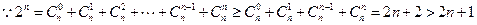
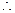 当
当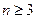 时,有
时,有 …………………..12分
…………………..12分
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
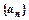 中,
中,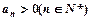 ,公比
,公比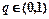 ,且
,且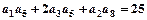 ,又
,又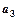 与
与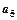 的等比中项为
的等比中项为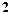 ,
,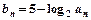 ,数列
,数列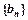 的前
的前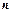 项和为
项和为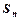 ,求数列
,求数列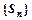 的通项公式
的通项公式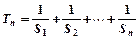 ,求
,求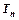
 an=(n∈N*),数列{bn}满足bn=n·ax'|x=n(其中ax'|x=n表示函数y=ax在x=n时的导数),则(ni=1bi)=( )
an=(n∈N*),数列{bn}满足bn=n·ax'|x=n(其中ax'|x=n表示函数y=ax在x=n时的导数),则(ni=1bi)=( ) 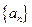 中,
中,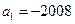 ,其前
,其前
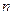 项的和为
项的和为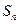 .若
.若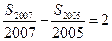 ,则
,则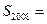 ( )
( )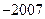
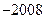
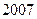
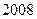
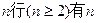 个数,且两端的数都是
个数,且两端的数都是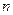 ,其余的每一个数都等于它肩上两个数的和,则第
,其余的每一个数都等于它肩上两个数的和,则第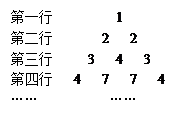
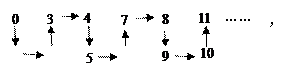
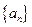 的前
的前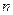 项和
项和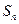 满足
满足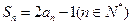 ,那么数列
,那么数列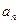 = .
= .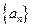 满足
满足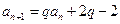 (
(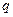 为常数,
为常数,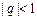 ),若
),若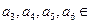
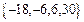 ,则
,则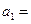 ▲ .
▲ .