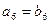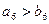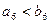题目内容
已知数列{an}的通项公式为 an=(n∈N*),数列{bn}满足bn=n·ax'|x=n(其中ax'|x=n表示函数y=ax在x=n时的导数),则(ni=1bi)=( )
an=(n∈N*),数列{bn}满足bn=n·ax'|x=n(其中ax'|x=n表示函数y=ax在x=n时的导数),则(ni=1bi)=( )
 an=(n∈N*),数列{bn}满足bn=n·ax'|x=n(其中ax'|x=n表示函数y=ax在x=n时的导数),则(ni=1bi)=( )
an=(n∈N*),数列{bn}满足bn=n·ax'|x=n(其中ax'|x=n表示函数y=ax在x=n时的导数),则(ni=1bi)=( ) | A.ln3 | B.-ln3 | C.-3ln3 | D.3ln3 |
B
ax=2×3-x,故ax'=2×3-xln3×(-1)=-2×3-xln3,即 bn=-,记 Tn=ni=1bi=(-2ln3)() , ①
∴ 3Tn=(-2ln3)(1+) 。 ②
②-①得:2Tn=(-2ln3)(1+),可得:Tn=-ln3[(1-]于是(ni=1bi)=Tn=-ln3.
∴ 3Tn=(-2ln3)(1+) 。 ②
②-①得:2Tn=(-2ln3)(1+),可得:Tn=-ln3[(1-]于是(ni=1bi)=Tn=-ln3.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 数列
数列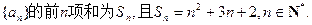
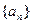 的通项公式;
的通项公式;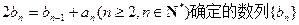 能否为等差数列?若能,求
能否为等差数列?若能,求 的值;若不能,说明理由。
的值;若不能,说明理由。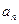 }、{
}、{ 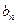 }满足:
}满足: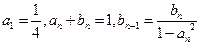 .
.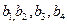 ; (2) 猜想
; (2) 猜想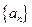 的通项公式,并用数学归纳法证明;
的通项公式,并用数学归纳法证明;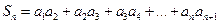 ,求实数
,求实数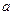 为何值时
为何值时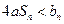 恒成立
恒成立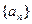 的前n项和为
的前n项和为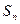 ,
,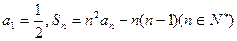
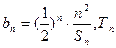 为数列
为数列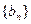 的前n项和,试比较
的前n项和,试比较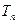 与
与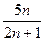 的大小,并加以证明
的大小,并加以证明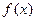 为偶函数,且
为偶函数,且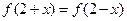 ,当
,当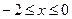 时,
时,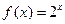 ;若
;若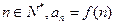 ,则
,则 (
(  )
)
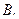
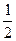
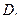
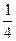
 的前
的前 项和为
项和为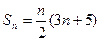 ,正项等比数列
,正项等比数列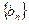 中,
中,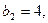
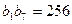 .
.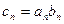 ,求
,求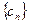 的前
的前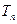 .
.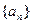 满足对于任意
满足对于任意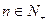 都有
都有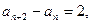 且
且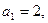 则
则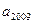 =( )
=( )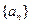 的通项公式为
的通项公式为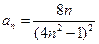 ,
,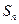 为其前
为其前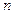 项的和.计算
项的和.计算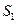 ,
,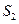 ,
,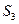 的值,根据计算结果,推测出计算
的值,根据计算结果,推测出计算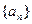 是等差数列,
是等差数列,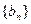 是等比数列,公比
是等比数列,公比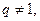 且
且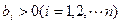 ,若
,若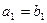 ,
,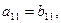 则( )
则( )