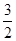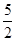题目内容
点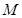 的直角坐标是
的直角坐标是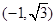 ,则点
,则点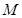 的极坐标为( )
的极坐标为( )
A.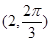 | B. |
C. | D.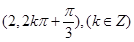 |
A
解析试题分析:利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,先将点M的直角坐标是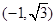 后化成极坐标即可.解:由于ρ2=x2+y2,得:ρ2=4,ρ=2,
后化成极坐标即可.解:由于ρ2=x2+y2,得:ρ2=4,ρ=2,
由ρcosθ=x得:cosθ=-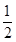 ,结合点在第二象限得:θ=
,结合点在第二象限得:θ=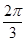 则点M的极坐标为
则点M的极坐标为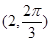 故选A.
故选A.
考点:极坐标和直角坐标的互化
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
抛物线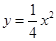 的焦点坐标是( )
的焦点坐标是( )
A.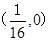 | B.(1,0) | C.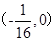 | D.(0,1) |
已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要实现不被曲线C挡住,则实数a的取值范围是( )
| A.(4,+∞) | B.(-∞,4) |
| C.(10,+∞) | D.(-∞,10) |
已知点P是以F1、F2为焦点的椭圆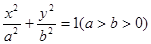 上一点,且
上一点,且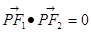 ,
,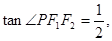 则该椭圆的离心率为( )
则该椭圆的离心率为( )
A.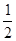 | B.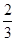 | C.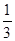 | D.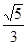 |
双曲线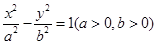 与直线
与直线 有公共点,则双曲线的离心率的取值范围是( )
有公共点,则双曲线的离心率的取值范围是( )
A.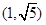 | B.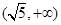 | C.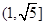 | D.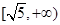 |
若方程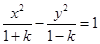 表示双曲线,则实数k的取值范围是 ( )
表示双曲线,则实数k的取值范围是 ( )
A. | B.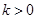 | C.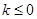 | D.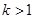 或 或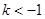 |
已知抛物线 的焦点为
的焦点为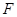 ,准线与
,准线与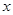 轴的交点为
轴的交点为 ,点
,点 在
在 上且
上且 ,则△
,则△ 的面积为( )
的面积为( )
| A.4 | B.8 | C.16 | D.32 |
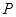 是双曲线
是双曲线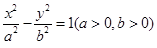 右支上一点,
右支上一点,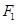 、
、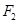 分别为双曲线的左、右焦点,点
分别为双曲线的左、右焦点,点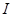 到△
到△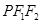 三边的距离相等,若
三边的距离相等,若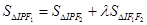 成立,则
成立,则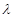 =
=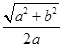
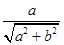
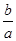
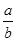
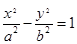 (
( )的两个焦点,若F1、F2、P(0,2
)的两个焦点,若F1、F2、P(0,2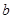 )是正三角形的三个顶点,则双曲线离心率是( )
)是正三角形的三个顶点,则双曲线离心率是( )