题目内容
已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要实现不被曲线C挡住,则实数a的取值范围是( )
| A.(4,+∞) | B.(-∞,4) |
| C.(10,+∞) | D.(-∞,10) |
D
解析试题分析:先看视线最高时为抛物线切线,而且为右上方向,设出切线的方程与抛物线方程联立消去y,根据判别式等于0求得k的值,进而求得切线的方程,把x=3代入即可求得y的值,B点只要在此切线下面都满足题意,进而求得a的范围.解:视线最高时为抛物线切线,而且为右上方向,设切线y=kx-2(k>0),与抛物线方程联立得2x2-kx+2=0,△=k2-16=0,k=4(负的舍去),∴切线为y=4x-2,取x=3得y=10,B点只要在此切线下面都满足题意∴a<10故选D.
考点:抛物线的简单性质
点评:本题主要考查了抛物线的简单性质,直线与抛物线的位置关系.考查了学生创造性思维能力和基本的分析推理能力

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知抛物线 焦点为
焦点为 ,过
,过 做倾斜角为
做倾斜角为 的直线,与抛物线交于A,B两点,若
的直线,与抛物线交于A,B两点,若 ,则
,则 = ( )
= ( )
A. | B. | C. | D. |
正方体  中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 到平面
到平面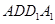 的距离是
的距离是 到直线
到直线 距离相等,则动点
距离相等,则动点 的轨迹为( )
的轨迹为( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
抛物线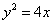 的焦点为F,点
的焦点为F,点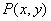 为该抛物线上的动点,又点
为该抛物线上的动点,又点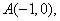 则
则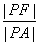 的最小值是
的最小值是
A.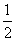 | B.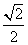 | C.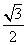 | D.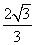 |
点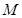 的直角坐标是
的直角坐标是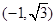 ,则点
,则点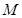 的极坐标为( )
的极坐标为( )
A.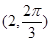 | B. |
C. | D.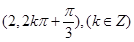 |
设 是等腰三角形,
是等腰三角形, ,则以
,则以 为焦点且过点
为焦点且过点 的双曲线的离心率为( )
的双曲线的离心率为( )
A. | B. | C. | D.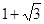 |
已知双曲线 的中心为原点,
的中心为原点, 是
是 的焦点,过
的焦点,过 的直线
的直线 与
与 相交于
相交于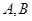 两点,且
两点,且 的中点为
的中点为 ,则
,则 的方程为( )
的方程为( )
A. | B. | C. | D. |
 ,则
,则 =( )
=( ) B.
B.  D.
D.
 上一点,设P到此抛物线准线的距离是d1,到直线
上一点,设P到此抛物线准线的距离是d1,到直线 的距离是d2,则dl+d2的最小值是( )
的距离是d2,则dl+d2的最小值是( )

