题目内容
已知抛物线 的焦点为
的焦点为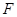 ,准线与
,准线与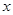 轴的交点为
轴的交点为 ,点
,点 在
在 上且
上且 ,则△
,则△ 的面积为( )
的面积为( )
| A.4 | B.8 | C.16 | D.32 |
B
解析试题分析:解:F(2,0)K(-2,0),过A作AM⊥准线,则|AM|=|AF|,∴|AK|=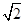 |AM|,∴△AFK的高等于|AM|,设A(m2,2
|AM|,∴△AFK的高等于|AM|,设A(m2,2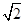 m)(m>0)则△AFK的面积=4×2
m)(m>0)则△AFK的面积=4×2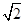 m•
m•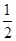 =4
=4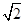 m又由|AK|=
m又由|AK|=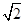 |AF|,过A作准线的垂线,垂足为P,三角形APK为等腰直角三角形,所以m=
|AF|,过A作准线的垂线,垂足为P,三角形APK为等腰直角三角形,所以m=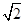 ∴△AFK的面积=4×2
∴△AFK的面积=4×2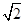 m•
m•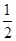 =8故答案为B
=8故答案为B
考点:抛物线的简单性质
点评:本题主要考查了抛物线的简单性质.考查了学生对抛物线基础知识的熟练掌握.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
点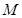 的直角坐标是
的直角坐标是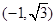 ,则点
,则点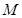 的极坐标为( )
的极坐标为( )
A.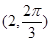 | B. |
C. | D.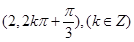 |
椭圆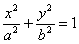
 的离心率是
的离心率是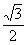 ,则双曲线
,则双曲线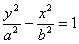 的渐近线方程是( )
的渐近线方程是( )
A.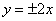 | B.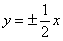 | C.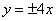 | D.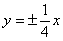 |
已知双曲线 的中心为原点,
的中心为原点, 是
是 的焦点,过
的焦点,过 的直线
的直线 与
与 相交于
相交于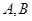 两点,且
两点,且 的中点为
的中点为 ,则
,则 的方程为( )
的方程为( )
A. | B. | C. | D. |
过双曲线的一个焦点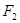 作垂直于实轴的弦
作垂直于实轴的弦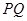 ,
,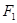 是另一焦点,若∠
是另一焦点,若∠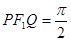 ,则双曲线的离心率
,则双曲线的离心率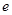 等于( )
等于( )
A. | B.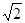 | C.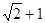 | D.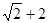 |
抛物线 的焦点为
的焦点为 ,点
,点 在抛物线上,且
在抛物线上,且 ,弦
,弦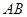 中点
中点 在准线
在准线 上的射影为
上的射影为 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
若抛物线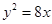 上一点
上一点 到其焦点的距离为
到其焦点的距离为 ,则点
,则点 的坐标为( )
的坐标为( )
A. | B. | C.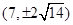 | D. |
 后,曲线C变为曲线
后,曲线C变为曲线 ,则曲线C的方程为 ( )
,则曲线C的方程为 ( ) 



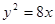 相切倾斜角为
相切倾斜角为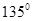 的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线 C.2 D.
C.2 D.