题目内容
已知圆 ,圆内有定点
,圆内有定点 ,圆周上有两个动点
,圆周上有两个动点 ,
, ,使
,使 ,则矩形
,则矩形 的顶点
的顶点 的轨迹方程为.
的轨迹方程为.

解析试题分析:设A( ),B(
),B( ),Q(
),Q(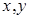 ),又P(1,1),
),又P(1,1),
则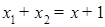 ,
, ,
, =(
=( ),
), =(
=( ).
).
由PA⊥PB,得 •
• =0,即(x1-1)(x2-1)+(y1-1)(y2-1)=0.
=0,即(x1-1)(x2-1)+(y1-1)(y2-1)=0.
整理得:x1x2+y1y2-(x1+x2)-(y1+y2)+2=0,
即x1x2+y1y2=x+1+y+1-2=x+y①
又∵点A、B在圆上,∴x12+y12=x22+y22=4②
再由|AB|=|PQ|,得(x1?y1)2+(x2?y2)2=(x?1)2+(y?1)2,
整理得:x12+y12+x22+y22?2(x1y1+x2y2)=(x?1)2+(y?1)2③
把①②代入③得:x2+y2=6.
∴矩形APBQ的顶点Q的轨迹方程为:x2+y2=6.
故答案为:x2+y2=6..
考点:直线与圆.

练习册系列答案
相关题目
 +4
+4 +8=0上的动点,PA、PB是圆
+8=0上的动点,PA、PB是圆 =0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
=0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 . 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数 的取值范围为 .
的取值范围为 . ,若
,若 ,则AB= .
,则AB= .
 上的点向圆
上的点向圆 引切线,则切线长的最小值为___________.
引切线,则切线长的最小值为___________.
 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,则圆
轴的正半轴建立平面直角坐标系,则圆 与圆
与圆 的值为_____________.
的值为_____________.