题目内容
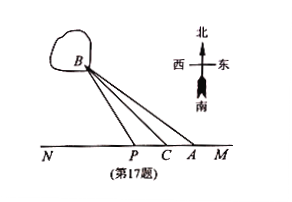
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|. 
(1)求实数a,b间满足的等量关系;
(2)若以P为圆心的圆P与圆O有公共点,试求圆P的半径最小时圆P的方程;
(3)当P点的位置发生变化时,直线QM是否过定点,如果是,求出定点坐标,如果不是,说明理由.
【答案】
(1)解:连OP,∵Q为切点,PQ⊥OQ,由勾股定理有|PQ|2=|OP|2﹣|OQ|2.
∵|PQ|=|PA|故PA2=PO2﹣1
∴a2+b2﹣1=(a﹣2)2+(b﹣1)2
化简可得,2a+b﹣3=0
(2)解:设圆P的半径为R,
∵圆P与圆O有公共点,且半径最小,
∴R=|OP|= ![]() =
= ![]() =
= ![]() ,
,
故当a= ![]() 时,|OP|min=
时,|OP|min= ![]()
此时,b= ![]() ,Rmin=
,Rmin= ![]() ﹣1.
﹣1.
得半径取最小值时圆P的方程为 ![]() ;
;
(3)解:设Q(x1,y1),M(x2,y2),则
 化简得ax1+by1=1,
化简得ax1+by1=1,
同理ax2+by2=1.
所以,直线MQ的方程为ax+by=1.
∵b=3﹣2a,代入上式得(x﹣2y)a+3y﹣1=0,
令x﹣2y=0,3y﹣1=0,得x= ![]() ,y=
,y= ![]() ,
,
∴直线MQ过定点( ![]() ).
).
【解析】(1)由已知Q为切点,可知PQ⊥OQ,结合勾股定理有|PQ|2=|OP|2﹣|OQ|2及已知|PQ|=|PA|,利用两点间的距离公式可得a,b之间的关系(2)设圆P的半径为R,由圆P与圆O有公共点,且半径最小,可知R=OP,利用两点间的距离,结合(1)中a,b的关系可转化为关于a的二次形式,结合二次函数的性质可求R的最小值,进而可求圆的方程;(3)求出直线MQ的方程,结合b=3﹣2a,即可得出结论.

【题目】已知函数f(x)=lnx.
(1)求函数g(x)=f(x+1)﹣x的最大值;
(2)若对任意x>0,不等式f(x)≤ax≤x2+1恒成立,求实数a的取值范围;
(3)若x1>x2>0,求证: ![]() >
> ![]() .
.
【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
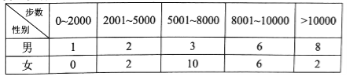
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?

附: ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.