题目内容
如图所示，已知圆O：x2+y2=1，直线l：y=kx+b(b＞0)是圆的一条切线，且l与椭圆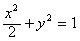
交于不同的两点A，B，
(Ⅰ)若△AOB的面积等于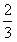
，求直线l的方程；
(Ⅱ)设△AOB的面积为S，且满足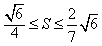
，求
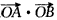的取值范围．
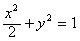交于不同的两点A，B，(Ⅰ)若△AOB的面积等于
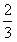，求直线l的方程；(Ⅱ)设△AOB的面积为S，且满足
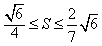，求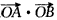的取值范围．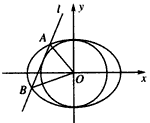
解：(Ⅰ)由题意可知：
，
∴
，
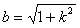由
，得
，
∴
，
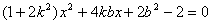而O到直线AB的距离为
，
则有
，得
，
所求直线l的方程为
。
(Ⅱ)由题意可知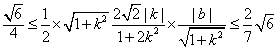
，
得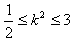
，
设A(x1，y1)，B(x2，y2)，
∴
=
，
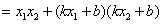
根据韦达定理得：
，
，
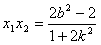代入上式得：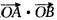
=
，
∴
。
，∴
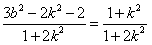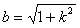，由
，得，∴
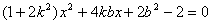，而O到直线AB的距离为
，则有
，得，所求直线l的方程为
。(Ⅱ)由题意可知
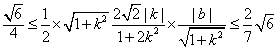，得
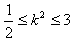，设A(x1，y1)，B(x2，y2)，
∴
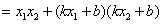
=，根据韦达定理得：
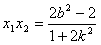，，代入上式得：
=， ∴
。 
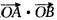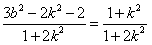练习册系列答案
相关题目
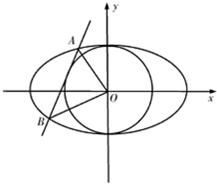如图所示，已知圆O：x2+y2=1，直线l：y=kx+b（b＞0）是圆的一条切线，且l与椭圆
如图所示，已知圆O：x2+y2=1，直线l：y=kx+b（k＞0，b＞0）是圆的一条切线，且l与椭圆
如图所示，已知圆O：x2+y2=4，直线m：kx-y+1=0．
（2013•肇庆一模）（几何证明选讲选做题）
（2012•衡阳模拟）如图所示，已知圆O直径AB=