题目内容
 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆| x2 |
| 2 |
(1)若弦AB的长为
| 4 |
| 3 |
(2)当直线l满足条件(1)时,求
| OA |
| OB |
分析:(1)由题意知b=
,又
,得(1+2k2)x2+4kbx+2b2-2=0,由此解得k=1或k=-1(舍).所以求直线l的方程为x-y+
=0.
(2)设A(x1,y1),B(x2,y2),∴
•
=x1x2+y1y2=2x1x2+
(x1+x2) +2,根据韦达定理得:x1+x2=-
,x1x2=
,由此得
•
=
.
| 1+k2 |
|
| 2 |
(2)设A(x1,y1),B(x2,y2),∴
| OA |
| OB |
| 2 |
| 4 |
| 3 |
| 2 |
| 2 |
| 3 |
| OA |
| OB |
| 2 |
| 3 |
解答:解:(1)由题意知:
=1,∴b=
,
又
,得(1+2k2)x2+4kbx+2b2-2=0,
∴|AB|=
•
=
,
解得k=1或k=-1(舍).
所以求直线l的方程为x-y+
=0.
(2)设A(x1,y1),B(x2,y2),∴
•
=x1x2+y1y2=2x1x2+
(x1+x2) +2,
根据韦达定理得:x1+x2=-
,x1x2=
,
代入上式,得
•
=
.
| |b| | ||
|
| 1+k2 |
又
|
∴|AB|=
| 1+k2 |
2
| ||
| 1+2k2 |
| 4 |
| 3 |
解得k=1或k=-1(舍).
所以求直线l的方程为x-y+
| 2 |
(2)设A(x1,y1),B(x2,y2),∴
| OA |
| OB |
| 2 |
根据韦达定理得:x1+x2=-
| 4 |
| 3 |
| 2 |
| 2 |
| 3 |
代入上式,得
| OA |
| OB |
| 2 |
| 3 |
点评:本题考查圆锥曲线和直线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
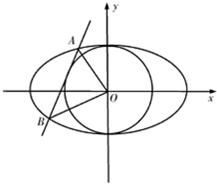 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆 如图所示,已知圆O:x2+y2=4,直线m:kx-y+1=0.
如图所示,已知圆O:x2+y2=4,直线m:kx-y+1=0. (2013•肇庆一模)(几何证明选讲选做题)
(2013•肇庆一模)(几何证明选讲选做题) (2012•衡阳模拟)如图所示,已知圆O直径AB=
(2012•衡阳模拟)如图所示,已知圆O直径AB=