题目内容
 如图所示,已知圆O:x2+y2=4,直线m:kx-y+1=0.
如图所示,已知圆O:x2+y2=4,直线m:kx-y+1=0.(1)求证:直线m与圆O有两个相异交点;
(2)设直线m与圆O的两个交点为A、B,求△AOB面积S的最大值.
分析:(1)根据该直线恒过点(0,1),而(0,1)在圆O:x2+y2=4内部,可得直线m与圆O有两个相异交点.
(2)求出圆心O到直线m的距离为 d、弦长AB的值,计算△AOB面积S=
|AB|×d=
,根据d的范围根据函数的单调性求得面积的最大值.
(2)求出圆心O到直线m的距离为 d、弦长AB的值,计算△AOB面积S=
| 1 |
| 2 |
| -(d2-2)2+4 |
解答:解析 (1)证明 直线m:kx-y+1=0可化为y-1=kx,
故该直线恒过点(0,1),而(0,1)在圆O:x2+y2=4内部,
所以直线m与圆O恒有两个不同交点.
(2)圆心O到直线m的距离为 d=
,而圆O的半径r=2,
故弦AB的长为|AB|=2
=2
,
故△AOB面积S=
|AB|×d=
×2
×d=
=
.
而d2=
,因为1+k2≥1,所以d2=
∈(0,1],
显然当d2∈(0,1]时,S单调递增,所以当d2=1,即k=0时,S取得最大值
,
此时直线m的方程为y-1=0.
故该直线恒过点(0,1),而(0,1)在圆O:x2+y2=4内部,
所以直线m与圆O恒有两个不同交点.
(2)圆心O到直线m的距离为 d=
| 1 | ||
|
故弦AB的长为|AB|=2
| r2-d2 |
| 4-d2 |
故△AOB面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4-d2 |
| 4d2-d4 |
| -(d2-2)2+4 |
而d2=
| 1 |
| 1+k2 |
| 1 |
| 1+k2 |
显然当d2∈(0,1]时,S单调递增,所以当d2=1,即k=0时,S取得最大值
| 3 |
此时直线m的方程为y-1=0.
点评:本题主要考查直线过定点问题,直线和圆的位置关系,点到直线的距离公式,利用函数的单调性求函数的值域,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
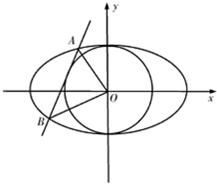 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆 (2013•肇庆一模)(几何证明选讲选做题)
(2013•肇庆一模)(几何证明选讲选做题) (2012•衡阳模拟)如图所示,已知圆O直径AB=
(2012•衡阳模拟)如图所示,已知圆O直径AB=