Question

【题目】已知在平面直角坐标系中,动点M到定点F(-,0)的距离与它到定直线l:x=-的距离之比为常数.

(1)求动点M的轨迹Γ的方程;

(2)设点A,若P是(1)中轨迹Γ上的动点,求线段PA的中点B的轨迹方程.

Answer 1

【答案】（1）；（2）

【解析】

（1）设动点坐标为，然后把已知条件用数学语言表示，化简后可得；

（2）设动点坐标为，用表示出点的坐标，再把点坐标代入（1）中轨迹方程后化简即可．

(1)设动点M(x,y),由已知可得=,即x2+2x+3+y2=,化简得+y2=1,即所求动点M的轨迹Γ的方程为+y2=1.

(2)设点B(x,y),点P(x0,y0),由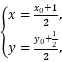得由点P在轨迹Γ上,得+=1,整理得+4=1,∴线段PA的中点B的轨迹方程是+4=1.