题目内容
设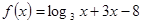 ,用二分法求方程
,用二分法求方程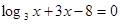 在区间
在区间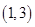 内的近似解中,取区间中点
内的近似解中,取区间中点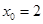 ,则下一个区间为 ( )
,则下一个区间为 ( )
| A.(1,2)或(2,3) | B.[1,2] | C.(1,2) | D.(2,3) |
D
解析试题分析 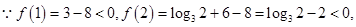
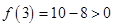 ,
,
所以下一个区间为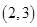
考点:函数零点的判定
点评:若函数在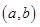 内连续且导数存在,则函数
内连续且导数存在,则函数 在
在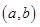 内存在零点的充要条件是
内存在零点的充要条件是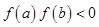 ,此题还可用函数方程的思想来求解:
,此题还可用函数方程的思想来求解: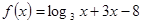 的零点即方程
的零点即方程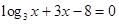 的根,进而转化为
的根,进而转化为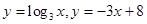 的交点横坐标,画出图像利用图像观察出结果,关于函数与方程的转化是高考考题中常出现的思路
的交点横坐标,画出图像利用图像观察出结果,关于函数与方程的转化是高考考题中常出现的思路

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知函数f(x)= 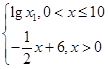 若a,b,c均不相等,且f(a)=" f(b)=" f(c),则abc的取值范围是( )
若a,b,c均不相等,且f(a)=" f(b)=" f(c),则abc的取值范围是( )
| A.(1,10) | B.(5,6) | C.(10,12) | D.(20,24) |
定义域为 的连续函数
的连续函数 ,对任意
,对任意 都有
都有 ,且其导函数
,且其导函数 满足
满足 ,则当
,则当 时,有( )
时,有( )
A. | B. |
C. | D. |
已知函数 在
在 处取得最大值,则( )
处取得最大值,则( )
A.函数 一定是奇函数 一定是奇函数 | B.函数 一定是偶函数 一定是偶函数 |
C.函数 一定是奇函数 一定是奇函数 | D.函数 一定是偶函数 一定是偶函数 |
在用二分法求方程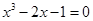 的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
| A.(1.4,2) | B.(1,1.4) | C.(1,1.5) | D.(1.5,2) |
设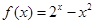 ,则在下列区间中使函数
,则在下列区间中使函数 有零点的区间是( )
有零点的区间是( )
A.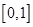 | B.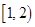 | C.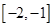 | D.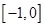 |
定义在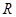 上的奇函数
上的奇函数 ,满足
,满足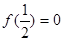 ,且在
,且在 上单调递减,则
上单调递减,则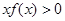 的解集为( )
的解集为( )
A.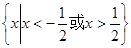 | B.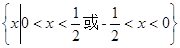 |
C.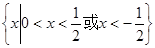 | D. |
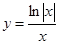 的图象大致是 ( )
的图象大致是 ( )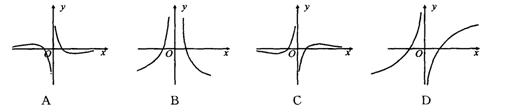
 的定义域是
的定义域是 ,则函数
,则函数 的定义域是 ( )
的定义域是 ( ) B.
B.  D.
D. 