ƒøƒ⁄»›
°æƒø°ø“—÷™≈◊ŒÔœflC£∫y2=2px£®p£æ0£©µƒΩπµ„Œ™F£¨AŒ™C…œ“Ï”⁄‘≠µ„µƒ»Œ“‚“ªµ„£¨π˝µ„Aµƒ÷±œfllΩªC”⁄¡Ì“ªµ„B£¨Ωªx÷·µƒ’˝∞Î÷·”⁄µ„D£¨«“”–ÿ≠FAÿ≠=ÿ≠FDÿ≠£Æµ±µ„Aµƒ∫·◊¯±ÍŒ™3 ±£¨°˜ADFŒ™’˝»˝Ω«–Œ£Æ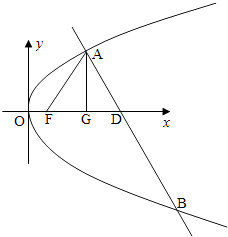
£®1£©«ÛCµƒ∑Ω≥ãª
£®2£©»Ù÷±œfll1°Œl£¨«“l1∫ÕC”–«“÷ª”–“ª∏ˆπ´π≤µ„E£¨
£®¢°£©÷§√˜÷±œflAEπ˝∂®µ„£¨≤¢«Û≥ˆ∂®µ„◊¯±Í£ª
£®¢¢£©°˜ABEµƒ√ʪ˝ «∑ҥʑ⁄◊Ó–°÷µ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ◊Ó–°÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø
£®1£©
Ω‚£∫µ±µ„Aµƒ∫·◊¯±ÍŒ™3 ±£¨π˝µ„A◊˜AG°Õx÷·”⁄G£¨
A£®3£¨ ![]() £©£¨F£®
£©£¨F£® ![]() £¨0£©£¨
£¨0£©£¨ ![]() £¨
£¨
°‡ ![]() £Æ
£Æ
°fl°˜ADFŒ™’˝»˝Ω«–Œ£¨
°‡ ![]() £Æ
£Æ
”÷°fl ![]() £¨
£¨
°‡ ![]() £¨
£¨
°‡p=2£Æ
°‡Cµƒ∑Ω≥ÃŒ™y2=4x£Æ
µ±D‘⁄Ωπµ„Fµƒ◊Û≤‡ ±£¨ ![]() £Æ
£Æ
”÷|FD|=2|FG|=2£® ![]() ©Å3£©=p©Å6£¨
©Å3£©=p©Å6£¨
°fl°˜ADFŒ™’˝»˝Ω«–Œ£¨
°‡3+ ![]() =p©Å6£¨Ω‚µ√p=18£¨
=p©Å6£¨Ω‚µ√p=18£¨
°‡Cµƒ∑Ω≥ÃŒ™y2=36x£Æ¥À ±µ„D‘⁄x÷·∏∫∞Î÷·£¨≤ª≥…¡¢£¨…·£Æ
°‡Cµƒ∑Ω≥ÃŒ™y2=4x£Æ
£®2£©
Ω‚£∫£®¢°£©…ËA£®x1£¨y1£©£¨|FD|=|AF|=x1+1£¨
°‡D£®x1+2£¨0£©£¨
°‡kAD=©Å ![]() £Æ
£Æ
”…÷±œfll1°Œlø……Ë÷±œfll1∑Ω≥ÃŒ™ ![]() £¨
£¨
¡™¡¢∑Ω≥à  £¨œ˚»•xµ√
£¨œ˚»•xµ√ ![]() ¢Ÿ
¢Ÿ
”…l1∫ÕC”–«“÷ª”–“ª∏ˆπ´π≤µ„µ√°˜=64+32y1m=0£¨°‡y1m=©Å2£¨
’‚ ±∑Ω≥⟵ƒΩ‚Œ™ ![]() £¨¥˙»Î
£¨¥˙»Î ![]() µ√x=m2£¨°‡E£®m2£¨2m£©£Æ
µ√x=m2£¨°‡E£®m2£¨2m£©£Æ
µ„Aµƒ◊¯±Íø…ªØŒ™ ![]() £¨÷±œflAE∑Ω≥ÃŒ™y©Å2m=
£¨÷±œflAE∑Ω≥ÃŒ™y©Å2m= ![]() £®x©Åm2£©£¨
£®x©Åm2£©£¨
º¥ ![]() £¨
£¨
°‡ ![]() £¨
£¨
°‡ ![]() £¨
£¨
°‡ ![]() £¨
£¨
°‡÷±œflAEπ˝∂®µ„£®1£¨0£©£ª
£®¢¢£©÷±œflABµƒ∑Ω≥ÃŒ™ ![]() £¨º¥
£¨º¥ ![]() £Æ
£Æ
¡™¡¢∑Ω≥à  £¨œ˚»•xµ√
£¨œ˚»•xµ√ ![]() £¨
£¨
°‡ ![]() £¨
£¨
°‡ ![]() =
= ![]() £¨
£¨
”…£®¢°£©µ„Eµƒ◊¯±ÍŒ™ ![]() £¨µ„EµΩ÷±œflABµƒæ‡¿ÎŒ™£∫
£¨µ„EµΩ÷±œflABµƒæ‡¿ÎŒ™£∫
 =
=  £¨
£¨
°‡°˜ABEµƒ√ʪ˝ ![]() =
= ![]() £¨
£¨
µ±«“Ωˆµ±y1=°¿2 ±µ»∫≈≥…¡¢£¨
°‡°˜ABEµƒ√ʪ˝◊Ó–°÷µŒ™16£Æ
°æΩ‚Œˆ°ø£®1£©∏˘æ›≈◊ŒÔœflµƒΩπ∞Îæ∂π´ Ω£¨Ω·∫œµ»±fl»˝Ω«–Œµƒ–‘÷ £¨«Û≥ˆµƒp÷µ£ª£®2£©£®¢°£©…Ë≥ˆµ„Aµƒ◊¯±Í£¨«Û≥ˆ÷±œflABµƒ∑Ω≥㨿˚”√÷±œfll1°Œl£¨«“l1∫ÕC”–«“÷ª”–“ª∏ˆπ´π≤µ„E£¨«Û≥ˆµ„Eµƒ◊¯±Í£¨–¥≥ˆ÷±œflAEµƒ∑Ω≥ã¨Ω´∑Ω≥ê،™µ„–± Ω£¨ø…«Û≥ˆ∂®µ„£ª£®¢¢£© ¿˚”√œ“≥§π´ Ω«Û≥ˆœ“ABµƒ≥§∂»£¨‘Ÿ«Ûµ„EµΩ÷±œflABµƒæ‡¿Î£¨µ√µΩπÿ”⁄√ʪ˝µƒ∫Ø ˝πÿœµ Ω£¨‘Ÿ¿˚”√ª˘±æ≤ªµ» Ω«Û◊Ó–°÷µ£Æ

 —ß¡∑øÏ≥µµ¿øÏ¿÷ºŸ∆⁄∫ƺŸ◊˜“µœµ¡–¥∞∏
—ß¡∑øÏ≥µµ¿øÏ¿÷ºŸ∆⁄∫ƺŸ◊˜“µœµ¡–¥∞∏ –¬ÀºŒ¨∫ƺŸ◊˜“µœµ¡–¥∞∏
–¬ÀºŒ¨∫ƺŸ◊˜“µœµ¡–¥∞∏