题目内容
已知递增数列{an}的通项公式是
，则实数λ的取值范围是（ ）
，则实数λ的取值范围是（ ）A． | B． | C． | D． |
D
解：∵，
∴
∵an是递增数列，
∴（n+1）2+λ（n+1）-n2-λn＞0
即2n+1+λ＞0
∴λ＞-2n-1
∵对于任意正整数都成立，
∴λ＞-3
故答案为：（-3，+∞）
，∴
∵an是递增数列，
∴（n+1）2+λ（n+1）-n2-λn＞0
即2n+1+λ＞0
∴λ＞-2n-1
∵对于任意正整数都成立，
∴λ＞-3
故答案为：（-3，+∞）
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
，
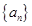满足
，
，
，且对任意的正整数
，当
时，都有
，则
的值是 
则
的值为
：
、
、
且
（
），与数列
：
、
、
、
且
（
．
，求
的值；
的值，并求证当
；
，且存在正整数
，使得在
，
，
，
中有4项为100.求
个图形包含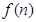
个小正方形.
，34,…中，
，则
.(用数值表示)
满足：
，则
=（ ）
，则其前n项的和等于 。