题目内容
1.已知函数f(x)=1nx-bx+c,f(x)在点(1,f(1))处的切线方程为x+y+4=0,f(x)的解析式为:f(x)=1nx-2x-3.分析 根据导数的几何意义求出函数在x=1处的导数,从而得到切线的斜率,建立等式关系,再根据切点在函数图象建立等式关系,解方程组即可求出a和b,从而得到函数f(x)的解析式;
解答 解:函数f(x)=1nx-bx+c,f(x)在点(1,f(1))处的切线方程为x+y+4=0,
f′(x)=$\frac{1}{x}$-b,f′(1)=1-b=-1.解得b=2,
又x=1,y=-5在f(x)的图象上,
∴0-2+c=-5.
得c=-3,b=2,
∴f(x)=1nx-2x-3.
故答案为:f(x)=1nx-2x-3.
点评 本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
10.(1+x)+(1+x)2+…+(1+x)n的所有二项式的各项系数和是( )
| A. | 2n+1 | B. | 2n+1+1 | C. | 2n+1-1 | D. | 2n+1-2 |
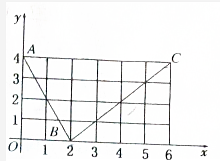 如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).
如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).