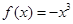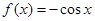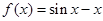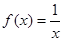题目内容
函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的
一个极值点,则下列图象不可能为y=f(x)的图象是 ( ).
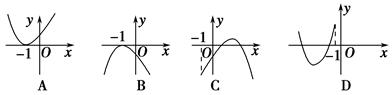
一个极值点,则下列图象不可能为y=f(x)的图象是 ( ).

D
设h(x)=f(x)ex,则h′(x)=(2ax+b)ex+(ax2+bx+c)ex=(ax2+2ax+bx+b+c)ex,由x=-1为函数f(x)ex的一个极值点,得h′(-1)=0.
即a-2a-b+b+c=0,∴c=a.
f(x)=ax2+bx+a.若方程ax2+bx+a=0有两个根x1,x2,则x1x2=1.D图中一定不满足该条件.
即a-2a-b+b+c=0,∴c=a.
f(x)=ax2+bx+a.若方程ax2+bx+a=0有两个根x1,x2,则x1x2=1.D图中一定不满足该条件.

练习册系列答案
相关题目
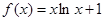
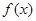 在
在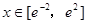 上的最大值与最小值;
上的最大值与最小值;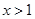 时,函数
时,函数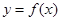 的图像恒在直线
的图像恒在直线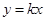 上方,求实数
上方,求实数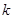 的取值范围;
的取值范围;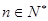 时,
时,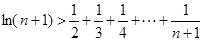 .
.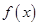 的定义域为
的定义域为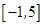 ,部分对应值如下表,
,部分对应值如下表,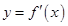 的图象如图所示.下列关于
的图象如图所示.下列关于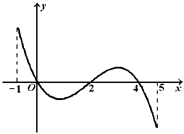
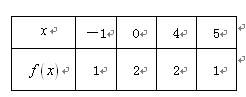
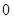 ,
, ;
;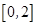 上是减函数;
上是减函数;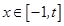 时,
时,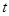 的最大值为4;
的最大值为4;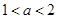 时,函数
时,函数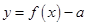 有
有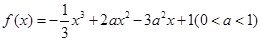 ,
,  的极大值;
的极大值;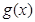 ,若
,若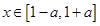 时,恒有
时,恒有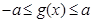 成立,试确定实数
成立,试确定实数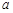 的取值范围.
的取值范围.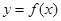 的导函数存在,则函数
的导函数存在,则函数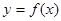 在一点的导数值为
在一点的导数值为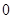 是函数
是函数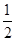 x2-2x+5,若对任意x∈[-1,2]有f(x)<m成立,则实数m的取值范围是________.
x2-2x+5,若对任意x∈[-1,2]有f(x)<m成立,则实数m的取值范围是________.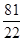
 是其极值点的函数是( )
是其极值点的函数是( )