题目内容
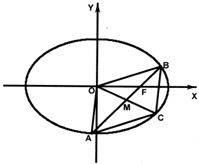 已知椭圆
已知椭圆| x2 |
| a2 |
(Ⅰ)设直线AB与直线OM的斜率分别为k1、k2,且k1•k2=-
| 1 |
| 2 |
(Ⅱ)若直线AB经过椭圆的右焦点F,且四边形OACB是平行四边形,求直线AB斜率的取值范围.
分析:(1)设A(x1,y1),B(x2,y2),C(x3,y3),则
,
+(y1+y2)(y1-y2)=0,
又x3=
,y3=
,k1=
,k2=
,再由k1•k2=-
能导出椭圆的离心率.
(2)由n=c,可知C(
,-
),代入椭圆方程,得4c2=m2+a2.由kAB2=
=
≤
,能导出k∈[-
,0)∪(0,
].
|
| (x1+x2)(x1-x2) |
| a2 |
又x3=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y1-y2 |
| x1-x2 |
| y3 |
| x3 |
| 1 |
| 2 |
(2)由n=c,可知C(
| 2a2c |
| m2+a2 |
| 2mc |
| m2+a2 |
| 1 |
| m2 |
| 1 |
| 3a2-4 |
| 1 |
| 8 |
| ||
| 4 |
| ||
| 4 |
解答:解:(1)设A(x1,y1),B(x2,y2),C(x3,y3),则
,两式相减,得:
+(y1+y2)(y1-y2)=0,
又x3=
,y3=
,k1=
,k2=
,
可得k2•k1=-
=-
,
∴a2=2,e=
.(5分)
(2)由n=c,可知C(
,-
),代入椭圆方程,得
4c2=m2+a2.(10分)
又c2=a2-1,a≥2,m≠0,
∴kAB2=
=
≤
,
∴k∈[-
,0)∪(0,
].(12分)
|
| (x1+x2)(x1-x2) |
| a2 |
又x3=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y1-y2 |
| x1-x2 |
| y3 |
| x3 |
可得k2•k1=-
| 1 |
| a2 |
| 1 |
| 2 |
∴a2=2,e=
| ||
| 2 |
(2)由n=c,可知C(
| 2a2c |
| m2+a2 |
| 2mc |
| m2+a2 |
4c2=m2+a2.(10分)
又c2=a2-1,a≥2,m≠0,
∴kAB2=
| 1 |
| m2 |
| 1 |
| 3a2-4 |
| 1 |
| 8 |
∴k∈[-
| ||
| 4 |
| ||
| 4 |
点评:本题考查椭圆的离心率的求法和直线的取值范围的求法.解题时要认真审题,注意椭圆性质的灵活运用,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目