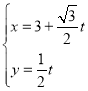题目内容
【题目】已知椭圆
右焦点与抛物线
的焦点重合，以原点为圆心、椭圆短半轴长为半径的圆与直线
相切.
（1）求椭圆的方程
（2）若直线
与y轴交点为P，A、B是椭圆上两个动点，它们在y轴两侧，
，
的平分线与y轴重合，则直线AB是否过定点，若过定点，求这个定点坐标，若不过定点说明理由.
【答案】（1）
；（2）存在，定点为
【解析】
（1）利用椭圆与抛物线焦点重合，先求出
，然后根据直线与圆的切线关系求得椭圆的短半径
即可
（2）利用
，求出直线
及其与y轴交点
，
可设椭圆上A、B两个动点的坐标为：
、
，然后，设AB方程为：
，通过直线与椭圆的联立方程求出
和
，最后，利用
的平分线在y轴上，得
，进而求出
，然后把代入直线即可求得该直线必过的定点
（1）抛物线
的焦点为
，所以
∵直线：
与圆
相切，
∴
，∴
∵椭圆C的方程是.
（2），直线与y轴交点
设椭圆上A、B两个动点的坐标为：、.
AB方程为：，
由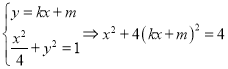
得：
，
，
得：
，
同理
又的平分线在y轴上
∵
，∴
，
，
直线
恒过定点.
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
